Question

【题目】如图①，在长方形ABCD中，AB=DC=3cm，BC=5cm，点P从点B出发，以1 cm/s的速度沿BC向点C运动，设点P的运动时间为ts.

（1）PC= cm（用含t的代数式表示）

（2）当t为何值时，△ABP≌△DCP，请说明理由

（3）如图②，当点P从点B开始运动时，点Q从点C出发，以a cm/s的速度沿CD向点D运动，是否存在这样a的值，使得△ABP与△PCQ全等?若存在，请求出a的值，若不存在，请说明理由。

Answer 1

【答案】（1）5t；（2）t=2.5 （3）a=1或a=1.2

【解析】分析: （1）根据题意求出BP，计算即可；

（2）根据全等三角形的判定定理解答；

（3）分△ABP≌△QCP和△ABP≌△PCQ两种情况，根据全等三角形的性质解答.

详解:

（1）∵点P的速度是1cm/s，

∴ts后BP=tcm，

∴PC=BCBP=(5t)cm，

（2）当t=2.5时,△ABP≌△DCP，

∵当t=2.5时，BP=CP=2.5，

在△ABP和△DCP中，

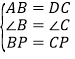
∴△ABP≌△DCP；

（3）∵∠B=∠C=90°，

∴当AB=PC,BP=CQ时,△ABP≌△PCQ，

∴5t=3，t=at，

解得，t=2，a=1，

当AB=QC,BP=CP时,△ABP≌△QCP，

此时，点P为BC的中点，点Q与点D重合，

∴t=2.5，at=3，

解得，a=1.2，

综上所述，当a=1或a=1.2时，△ABP与△PCQ全等。

点睛: 本题考查的是矩形的性质、全等三角形的判定和性质，掌握矩形的对边相等、四个角都是直角以及全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.