题目内容
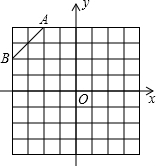
如图,在规格为8×8的正方形网格中建立平面直角坐标系,请在所给网格中按下列要求操作:(1)直接写出A、B两点的坐标;
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标;
(3)以(2)中△ABC的顶点C为旋转中心,画出△ABC旋转180°后所得到的△DEC,连接AE和BD,试判定四边形ABDE是什么特殊四边形,并说明理由.

【答案】分析:(1)A、B两点位于第二象限内,根据第二象限内点的坐标特征,可以写出A,B两点的坐标分别是:A(-2,4),B(-4,2).
(2)以AB为底的等腰三角形在第二象限有无数个,由于题目要求在格点上找,所以有(-4,4),(-2,2)以及(-1,1)三个点,而前两个点,腰长为2,不符合要求,所以点C的坐标只能是(-1,1),其腰长为 .
.
(3)画出图示如图,根据(2)中的结论,可以求出AD=BE,且AC=BC=CD=CE,根据矩形的判定定理,可以判定四边形是矩形.
解答:解:(1)根据图示,点A和B的坐标分别是A(-2,4),B(-4,2).
(2)点C的坐标是(-1,1),
根据图示可得,腰长CB=CA=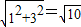 .
.
 是无理数,符合要求.
是无理数,符合要求.
(3)画出旋转后的图形如图所示,

由于旋转180°,所以A、C、D共线,同理,B、C、E共线,
根据题意知,AC=BC=CD=CE= ,
,
∴AD=BE,
∴四边形ABDE是矩形.
点评:本题是一个综合题,结合坐标系,考查了旋转的知识,同时还考查了特殊四边形的判定.
(2)以AB为底的等腰三角形在第二象限有无数个,由于题目要求在格点上找,所以有(-4,4),(-2,2)以及(-1,1)三个点,而前两个点,腰长为2,不符合要求,所以点C的坐标只能是(-1,1),其腰长为
 .
.(3)画出图示如图,根据(2)中的结论,可以求出AD=BE,且AC=BC=CD=CE,根据矩形的判定定理,可以判定四边形是矩形.
解答:解:(1)根据图示,点A和B的坐标分别是A(-2,4),B(-4,2).
(2)点C的坐标是(-1,1),
根据图示可得,腰长CB=CA=
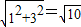 .
. 是无理数,符合要求.
是无理数,符合要求.(3)画出旋转后的图形如图所示,

由于旋转180°,所以A、C、D共线,同理,B、C、E共线,
根据题意知,AC=BC=CD=CE=
 ,
,∴AD=BE,
∴四边形ABDE是矩形.
点评:本题是一个综合题,结合坐标系,考查了旋转的知识,同时还考查了特殊四边形的判定.

练习册系列答案
相关题目
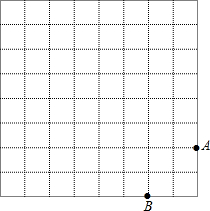 如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作: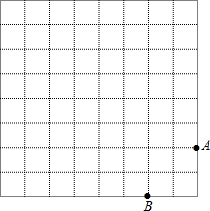 如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作: