��Ŀ����
����Ϊ1����Ϊa�ij�����ֽƬ��
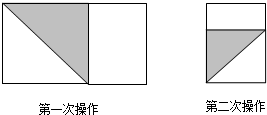
��a��1����ͼ������һ�£�����һ���߳����ڳ����ο��ȵ������Σ���Ϊ��һ�β��������ٰ�ʣ�µij�������ͼ������һ�£�����һ���߳����ڴ�ʱ���ο��ȵ������Σ���Ϊ�ڶ��β���������˷���������ȥ�����ڵ�n�β�����ʣ�µľ���Ϊ�����Σ��������ֹ��
��1����һ�β�����ʣ�µľ������߳��ֱ�Ϊ
��2�����ڶ��β�����ʣ�µij�����ǡ���������Σ���a=
��
��3���������β�����ʣ�µij�����ǡ���������Σ�����a��ֵ��
| 1 |
| 2 |
��1����һ�β�����ʣ�µľ������߳��ֱ�Ϊ
a��1-a
a��1-a
�����ú�a�Ĵ���ʽ��ʾ����2�����ڶ��β�����ʣ�µij�����ǡ���������Σ���a=
| 2 |
| 3 |
| 2 |
| 3 |
��3���������β�����ʣ�µij�����ǡ���������Σ�����a��ֵ��

��������1������������ͼ�ο��Կ���ÿһ�β���ʱ���������εı߳�������ԭ���εĿ����ٸ��ݳ�Ϊ1����Ϊa�ij����μ��ɵó�ʣ�µij����εij��Ϳ���
��2���ٸ��ݣ�1�����ó���ԭ�����ó��ڶ��β���ʱ�����εı߳�Ϊ1-a����������ڶ��β����Ժ�ʣ�µľ��ε����ߵij��ֱ���1-a��2a-1������ʣ�µij�����ǡ���������Σ��������a��ֵ��
��3�����ݣ�2�����ó��ij��������߳��ֱ���1-a��2a-1������������������ۣ��ٵ�1-a��2a-1ʱ�������β�����ʣ�µij��������߳��ֱ��ǣ�1-a��-��2a-1����2a-1���ڵ�1-a��2a-1ʱ�������β�����ʣ�µij��������߳��ֱ��ǣ�2a-1��-��1-a����1-a������ʣ�µij�����ǡ���������Σ��������a��ֵ��
��2���ٸ��ݣ�1�����ó���ԭ�����ó��ڶ��β���ʱ�����εı߳�Ϊ1-a����������ڶ��β����Ժ�ʣ�µľ��ε����ߵij��ֱ���1-a��2a-1������ʣ�µij�����ǡ���������Σ��������a��ֵ��
��3�����ݣ�2�����ó��ij��������߳��ֱ���1-a��2a-1������������������ۣ��ٵ�1-a��2a-1ʱ�������β�����ʣ�µij��������߳��ֱ��ǣ�1-a��-��2a-1����2a-1���ڵ�1-a��2a-1ʱ�������β�����ʣ�µij��������߳��ֱ��ǣ�2a-1��-��1-a����1-a������ʣ�µij�����ǡ���������Σ��������a��ֵ��
����⣺��1���߳�Ϊ1����Ϊa�ij�����ֽƬ��
��a��1����
���һ�β�����ʣ�µľ��εij�Ϊa����Ϊ1-a��
��2���ߵڶ��β���ʱ�����εı߳�Ϊ1-a���ڶ��β����Ժ�ʣ�µľ��ε����߷ֱ�Ϊ1-a��2a-1��
��ʱ����ǡ���������Σ�
��1-a=2a-1��
���a=
��
��3���ڶ��β�����ʣ�¾��ε����߳��ֱ�Ϊ��1-a��2a-1��
�ٵ�1-a��2a-1ʱ��
��������1-a��-��2a-1��=2a-1��
��ã�a=
��
��a=
ʱ��1-a��2a-1�����ԣ�a=
�������һ��ֵ��
�ڵ�1-a��2a-1ʱ��
��������2a-1��-��1-a��=1-a��
��ã�a=
��
��a=
ʱ��1-a��2a-1�����ԣ�a=
�������һ��ֵ��
���ԣ�����a��ֵΪ
��
��
�ʴ�Ϊ��1��a��1-a����2��
��
| 1 |
| 2 |
���һ�β�����ʣ�µľ��εij�Ϊa����Ϊ1-a��
��2���ߵڶ��β���ʱ�����εı߳�Ϊ1-a���ڶ��β����Ժ�ʣ�µľ��ε����߷ֱ�Ϊ1-a��2a-1��
��ʱ����ǡ���������Σ�
��1-a=2a-1��
���a=
| 2 |
| 3 |
��3���ڶ��β�����ʣ�¾��ε����߳��ֱ�Ϊ��1-a��2a-1��
�ٵ�1-a��2a-1ʱ��
��������1-a��-��2a-1��=2a-1��
��ã�a=
| 3 |
| 5 |
��a=
| 3 |
| 5 |
| 3 |
| 5 |
�ڵ�1-a��2a-1ʱ��
��������2a-1��-��1-a��=1-a��
��ã�a=
| 3 |
| 4 |
��a=
| 3 |
| 4 |
| 3 |
| 4 |
���ԣ�����a��ֵΪ
| 3 |
| 5 |
| 3 |
| 4 |
�ʴ�Ϊ��1��a��1-a����2��
| 2 |
| 3 |
���������⿼����һԪһ�η��̵�Ӧ�ã�����Ĺؼ��Ƿֱ����ÿ�β�����ʣ�µľ��ε����ߵij��ȣ���һ���Ѷȣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
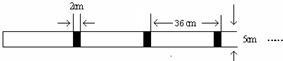

 ��ͼ������һ�£�����һ���߳����ڳ����ο��ȵ������Σ���Ϊ��һ�β��������ٰ�ʣ�µij�������ͼ������һ�£�����һ���߳����ڴ�ʱ���ο��ȵ������Σ���Ϊ�ڶ��β�������
��ͼ������һ�£�����һ���߳����ڳ����ο��ȵ������Σ���Ϊ��һ�β��������ٰ�ʣ�µij�������ͼ������һ�£�����һ���߳����ڴ�ʱ���ο��ȵ������Σ���Ϊ�ڶ��β�������
