题目内容
将长为1,宽为a的长方形纸片(
<a<1)如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作).
(1)第一次操作后,剩下的长方形的长和宽分别为多少?(用含a的代数式表示)
(2)第二次操作后,剩下的长方形的面积是多少?(列出代数式,不需化简)
(3)假如第二次操作后,剩下的长方形恰好是正方形,则a的值是多少?

| 1 | 2 |
(1)第一次操作后,剩下的长方形的长和宽分别为多少?(用含a的代数式表示)
(2)第二次操作后,剩下的长方形的面积是多少?(列出代数式,不需化简)
(3)假如第二次操作后,剩下的长方形恰好是正方形,则a的值是多少?

分析:(1)根据所给的图形可以看出每一次操作时所得正方形的边长都等于原矩形的宽,再根据长为1,宽为a的长方形即可得出剩下的长方形的长和宽;
(2)再根据(1)所得出的原理,得出第二次操作时正方形的边长为1-a,即可求出第二次操作以后剩下的矩形的两边的长,再根据面积公式即可得出答案;
(3)根据(2)所得出的长方形两边长分别是1-a和2a-1,并且剩下的长方形恰好是正方形,即可求出a的值.
(2)再根据(1)所得出的原理,得出第二次操作时正方形的边长为1-a,即可求出第二次操作以后剩下的矩形的两边的长,再根据面积公式即可得出答案;
(3)根据(2)所得出的长方形两边长分别是1-a和2a-1,并且剩下的长方形恰好是正方形,即可求出a的值.
解答:解:(1)∵长为1,宽为a的长方形纸片(
<a<1),
∴第一次操作后剩下的矩形的长为a,宽为1-a;
(2)∵第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1,
∴剩下的长方形的面积是(1-a)(2a-1);
(3)根据(2)所得,第二次操作后剩下的长方形两边长分别是1-a和2a-1,
当剩下的长方形恰好是正方形时,即1-a=2a-1,
解得:a=
.
| 1 |
| 2 |
∴第一次操作后剩下的矩形的长为a,宽为1-a;
(2)∵第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1,
∴剩下的长方形的面积是(1-a)(2a-1);
(3)根据(2)所得,第二次操作后剩下的长方形两边长分别是1-a和2a-1,
当剩下的长方形恰好是正方形时,即1-a=2a-1,
解得:a=
| 2 |
| 3 |
点评:本题考查了一元一次方程的应用,解题的关键是分别求出每次操作后剩下的矩形的两边的长度.

练习册系列答案
相关题目
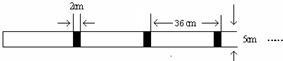
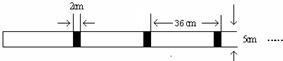
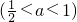 如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作).
如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作).
