题目内容
【题目】如图,在平面直角坐标系中,点A在x轴的负半轴上,B点坐标为(6,0),点C在y轴的负半轴上,且OB=OC,抛物线y=![]() x2+bx+c经过A、B、C三点.
x2+bx+c经过A、B、C三点.
(1)求此抛物线的函数关系式和点A的坐标;
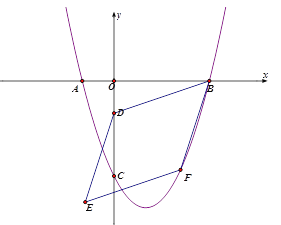
(2)点D的坐标为(0,-2),F为该二次函数图像上的动点,连接BD、BF,以BD、BF为邻边作平行四边形BDEF,
①若点F为该二次函数在第四象限图像上的动点,设平行四边形BDEF的面积为S。求S的最大值。
②在点F的运动过程中,当点E落在一次函数y=x+7上时,求点F的坐标。
【答案】(1)y=![]() x2-x-6 ; A(-3,0);(2)①32;②F1(-3,0)F2(9,12)
x2-x-6 ; A(-3,0);(2)①32;②F1(-3,0)F2(9,12)
【解析】试题分析:(1)由OC=OB可得点C的坐标为(0,-6),再将点B、C的坐标代入抛物线y=![]() x2+bx+c中,即可得出抛物线的解析式,当y=0 时,求得x1=-3,x2=6,即点A的坐标为(-3,0);
x2+bx+c中,即可得出抛物线的解析式,当y=0 时,求得x1=-3,x2=6,即点A的坐标为(-3,0);
(2)①连接OF、DF,设点F的坐标为(t, ![]() 2-t-6),根据S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF求得
2-t-6),根据S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF求得![]() =-(t-2)2+16,由四边形BDEF是平行四边形得
=-(t-2)2+16,由四边形BDEF是平行四边形得![]() =
=![]() ,所以当
,所以当![]() 面积最大时,平行四边形BDEF的面积为S也有最大值.由
面积最大时,平行四边形BDEF的面积为S也有最大值.由![]() =-(t-2)2+16得:当t=2时,S△BDF有最大值=16,即平行四边形BDEF的面积S的最大值 为32.
=-(t-2)2+16得:当t=2时,S△BDF有最大值=16,即平行四边形BDEF的面积S的最大值 为32.
②设E点坐标为(m,m+7),由BD//EF,且BD=EF,则由D(0,-2)平移到B(6,0),则点E(m,m+7)平移到F(m+6,m+9),将F(m+6,m+9)代入y=![]() x2-x-6得m+9=
x2-x-6得m+9=![]() (m+6)2-(m+6)-6,即可求得m的值,即可求得F的坐标;
(m+6)2-(m+6)-6,即可求得m的值,即可求得F的坐标;
试题解析:
(1)∵OB=OC,B点坐标为(6,0),
∴点C坐标为(0,-6),
∵点B、C在抛物线y=![]() x2+bx+c上,
x2+bx+c上,
∴![]()
解得![]() ,
,
∴抛物线的解析式为:y=![]() x2-x-6
x2-x-6
当y=0时,即![]() x2-x-6 =0,解得x1=-3,x2=6,
x2-x-6 =0,解得x1=-3,x2=6,
所以A(-3
(2) ①连接OF、DF,如图所示:
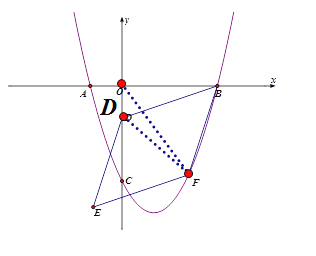
设点F的坐标为(t, ![]() 2-t-6),
2-t-6),
∴S△OBD+S△BDF =![]() ,
,
SODF+S△OBF=![]()
![]()
![]()
又∵S四边形OBFD=S△OBD+S△BDF=SODF+S△OBF
∴![]() =
=![]() ,即
,即![]() =
=![]() =-(t-2)2+16
=-(t-2)2+16
∵四边形BDEF是平行四边形,
∴![]() =
=![]() ,
,
∴当![]() 面积最大时,平行四边形BDEF的面积为S也有最大值.
面积最大时,平行四边形BDEF的面积为S也有最大值.
当t=2时,S△BDF有最大值=16,
∴平行四边形BDEF的面积S的最大值 为32.
当x=2时,S的最大值为32
②设E点坐标为(m,m+7),
∵BD//EF,且BD=EF,则由D(0,-2)平移到B(6,0),
∴点E(m,m+7)平移到F(m+6,m+9),
将F(m+6,m+9)代入y=![]() x2-x-6得m+9=
x2-x-6得m+9=![]() (m+6)2-(m+6)-6,
(m+6)2-(m+6)-6,
解得:m1=-9,m2=3,
所以F1(-3,0)或F2(9,12).