题目内容
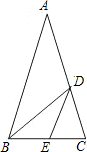顶角为36°的等腰三角形称为黄金三角形．如图，△ABC、△BDC、△DEC都是黄金三角形，已知AB=1，则DE=分析：根据相似比求解．
解答：解：∵△ABC、△BDC、△DEC都是黄金三角形，AB=1
∴AB=AC，AD=BD=BC，DE=BE=CD，DE∥AB
∴设DE=x，则CD=BE=x，AD=BC=1-x，
=
∴EC=BC-BE=1-x-x=1-2x
∴
=
解得：DE=
．
∴AB=AC，AD=BD=BC，DE=BE=CD，DE∥AB
∴设DE=x，则CD=BE=x，AD=BC=1-x，
| DE |
| AB |
| EC |
| BC |
∴EC=BC-BE=1-x-x=1-2x
∴
| x |
| 1 |
| 1-2x |
| 1-x |
解得：DE=
3-
| ||
| 2 |
点评：此题考查了相似三角形的性质与方程思想，相似三角形的对应边的比相等；解题时要注意方程思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
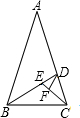如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫黄金三角形，已知腰长AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2007个黄金三角形的周长为（ ）| A、k2006 | ||
| B、k2007 | ||
C、
| ||
| D、k2006（2+k） |
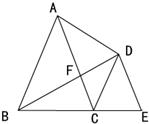20、已知：△ABC与△CDE都是顶角为36°的等腰三角形，BC=CD，AC与BD交于F，且B、C、E三点共线．
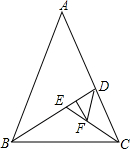如图所示，顶角为36°的等腰三角形，其底边与腰之比等于k，这样的三角形叫做黄金三角形．已知AB=1，△ABC为第一个黄金三角形，△BCD为第二个黄金三角形，△CDE为第三个黄金三角形，以此类推，第2014个黄金三角形的周长为（ ）