题目内容
【题目】已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)如图1所示,当∠DOE=20°时,∠FOH的度数是 .
(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.
(3)若再作射线OG平分∠BOF,试求∠GOH的度数.

【答案】(1)35°;(2)∠BOE=2∠FOH,理由详见解析;(3)45°或135°.
【解析】
(1)根据∠AOD=90![]() ,∠DOE=20
,∠DOE=20![]() 得∠AOE=∠AOD+∠DOE=110
得∠AOE=∠AOD+∠DOE=110![]() ,再根据OH平分∠AOE,即可求解;
,再根据OH平分∠AOE,即可求解;
(2)可以设∠AOH=x,根据OH平分∠AOE,可得∠HOE=∠AOH=x,进而∠FOH=90![]() ﹣∠HOE=90
﹣∠HOE=90![]() ﹣x,∠BOE=180
﹣x,∠BOE=180![]() ﹣∠AOE=180
﹣∠AOE=180![]() ﹣2x,即可得结论;
﹣2x,即可得结论;
(3)分两种情况解答:当OE落在∠BOD内时,OF落在∠AOD内,当OE落在其他位置时,根据OH平分∠AOE,OG平分∠BOF即可求解.
解:(1)因为∠AOD=90![]() ,∠DOE=20
,∠DOE=20![]()
所以∠AOE=∠AOD+∠DOE=110![]()
因为OH平分∠AOE
所以∠HOE=![]() AOE=55
AOE=55![]()
所以∠FOH=90![]() ﹣∠HOE=35
﹣∠HOE=35![]() ;
;
故答案为35![]() ;
;
(2)∠BOE=2∠FOH,理由如下:
设∠AOH=x,
因为OH平分∠AOE
所以∠HOE=∠AOH=x
所以∠FOH=90![]() ﹣∠HOE=90
﹣∠HOE=90![]() ﹣x
﹣x
∠BOE=180![]() ﹣∠AOE=180
﹣∠AOE=180![]() ﹣2x
﹣2x
所以∠BOE=2∠FOH;
(3)如图3,当OE落在∠BOD内时,OF落在∠AOD内
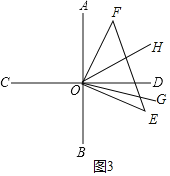
因为OH平分∠AOE
所以∠HOE=∠AOH=![]() AOE
AOE
因为OG平分∠BOF
∠FOG=∠GOB=![]() BOF
BOF
所以∠GOH=∠GOF﹣∠FOH
=![]() BOF﹣(∠AOH﹣∠AOF)
BOF﹣(∠AOH﹣∠AOF)
=![]() (180
(180![]() ﹣∠AOF)﹣
﹣∠AOF)﹣![]() AOE+∠AOF
AOE+∠AOF
=90![]() ﹣
﹣![]() AOF﹣
AOF﹣![]() (90
(90![]() +∠AOF)+∠AOF
+∠AOF)+∠AOF
=90![]() ﹣
﹣![]() AOF﹣45
AOF﹣45![]() ﹣
﹣![]() AOF+∠AOF
AOF+∠AOF
=45![]() ;
;
所以∠GOH的度数为45![]() ;
;
如图4,当OE落在其他位置时
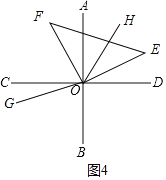
因为OH平分∠AOE
所以∠HOE=∠AOH=![]() AOE
AOE
因为OG平分∠BOF
∠FOG=∠GOB=![]() BOF
BOF
所以∠GOH=∠GOF+∠FOH
=![]() BOF+∠AOH+∠AOF
BOF+∠AOH+∠AOF
=![]() (180
(180![]() ﹣∠AOF)+
﹣∠AOF)+![]() AOE+∠AOF
AOE+∠AOF
=90![]() ﹣
﹣![]() AOF+
AOF+![]() (90
(90![]() ﹣∠AOF)+∠AOF
﹣∠AOF)+∠AOF
=90![]() ﹣
﹣![]() AOF+45
AOF+45![]() ﹣
﹣![]() AOF+∠AOF
AOF+∠AOF
=135![]() ;
;
所以∠GOH的度数为135![]() ;
;
综上所述:∠GOH的度数为45![]() 或135
或135![]() .
.