题目内容
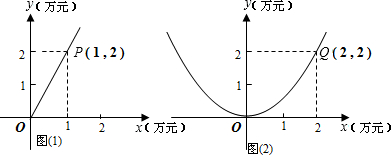
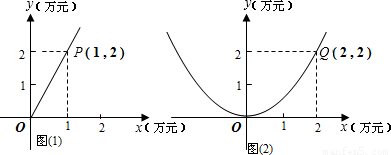
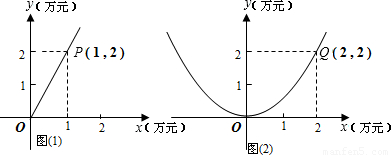
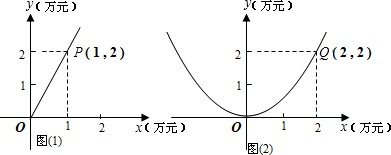
随着近几年经济的快速发展,人民生活水平逐步提高,市场对鱼肉的需求量逐年增大.某农场计划投资养殖鱼和生猪,根据市场调查与预测,养殖生猪的利润y1与投资量x成正比例关系,如图①所示;养殖鱼的利润y2与投资量x成二次函数关系,如图②所示(利润与投资量的单位:万元)(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果农场以8万元资金投入养殖鱼和生猪,农场至少获得多少利润?农场能获取的最大利润是多少?
分析:(1)根据直线,抛物线在坐标系的位置,合理地设函数解析式,都是直线,抛物线解析式的最简形式.(2)农场以8万元资金投入养殖鱼和生猪,设养殖鱼投资t万元,利润为y万元,则养殖生猪(8-t)万元,这里的利润是两项利润的和.利用二次函数的性质,求最大值.
解答:解:(1)设y1=kx(k≠0),
把P(1,2)坐标代入得k=2,
∴y1=2x;
设y2=ax2(a≠0),
把Q(2,2)代入得a=
,
∴y2=
x2
(2)设养殖鱼投资t万元,利润为y万元,则养殖生猪(8-t)万元.
根据题意得:y=y1+y2=2(8-t)+
t2=
t2-2t+16=
(t-2)2+14(0≤t≤8)
当t=2时,y最小值=14;当t=8时,y最大值=32
答:农场至少获得利润14万元;农场能获取的最大利润是32万元.
把P(1,2)坐标代入得k=2,
∴y1=2x;
设y2=ax2(a≠0),
把Q(2,2)代入得a=
| 1 |
| 2 |
∴y2=
| 1 |
| 2 |
(2)设养殖鱼投资t万元,利润为y万元,则养殖生猪(8-t)万元.
根据题意得:y=y1+y2=2(8-t)+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当t=2时,y最小值=14;当t=8时,y最大值=32
答:农场至少获得利润14万元;农场能获取的最大利润是32万元.
点评:所求二次函数自变量t有一定限制,图象也只是抛物线的一部分,求最大(最小)利润,需要在自变量取值范围内.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目