题目内容
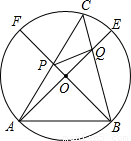
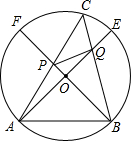 已知:如图,在直径为10的⊙O中,作两条互相垂直的直径AE和BF,在弧EF上取点C,弦AC交BF于P,弦CB交AE于Q,求证:四边形APQB的面积等于25.
已知:如图,在直径为10的⊙O中,作两条互相垂直的直径AE和BF,在弧EF上取点C,弦AC交BF于P,弦CB交AE于Q,求证:四边形APQB的面积等于25.分析:连接AF、FE、EB,设AC与EF交于点D,连接DB、DQ、CE,由于AE、BF是⊙O的直径,AE⊥BF,根据对角线互相垂直平分且相等的四边形为正方形得到四边形ABEF是正方形,则S△ABF=
S正方形ABEF=
×
×10×10=25,根据圆周角定理得到∠DCQ=
∠AOB=45°,而∠DEQ=45°,则∠DCQ=∠DEQ,根据四点共圆的判定方法得D、C、E、Q在同一个圆上;又AE是⊙O的直径,根据直径所对的圆周角为直角得到∠ACE=90°,再利用圆的内接四边形的性质得到∠DQE=180°-∠ACE=90°,则DQ⊥AE,易得FB∥DQ,
则S△PBQ=S△PBD,于是可得S四边形APQB=S△APB+S△QPB=S△PAB+S△DPB=S△DAB=S△FAB=25.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则S△PBQ=S△PBD,于是可得S四边形APQB=S△APB+S△QPB=S△PAB+S△DPB=S△DAB=S△FAB=25.
解答:证明:连接AF、FE、EB,设AC与EF交于点D,连接DB、DQ、CE,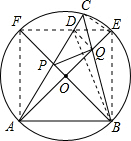 如图,
如图,
∵AE、BF是⊙O的直径,AE⊥BF,
∴四边形ABEF是正方形,
∴S△ABF=
S正方形ABEF=
×
×10×10=25,
又∵∠DCQ=
∠AOB=45°,
而∠DEQ=45°,
∴∠DCQ=∠DEQ,
∴D、C、E、Q在同一个圆上,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠DQE=180°-∠ACE=90°,
∴DQ⊥AE,
而AE⊥BF,
∴FB∥DQ,
∴S△PBQ=S△PBD,
∴S四边形APQB=S△APB+S△QPB=S△PAB+S△DPB=S△DAB=S△FAB=25.
 如图,
如图,∵AE、BF是⊙O的直径,AE⊥BF,
∴四边形ABEF是正方形,
∴S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠DCQ=
| 1 |
| 2 |
而∠DEQ=45°,
∴∠DCQ=∠DEQ,
∴D、C、E、Q在同一个圆上,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠DQE=180°-∠ACE=90°,
∴DQ⊥AE,
而AE⊥BF,
∴FB∥DQ,
∴S△PBQ=S△PBD,
∴S四边形APQB=S△APB+S△QPB=S△PAB+S△DPB=S△DAB=S△FAB=25.
点评:本题考查了圆的综合题:在同圆或等圆中,一条弧所对的圆周角的度数是它所对的圆心角的度数的一半;直径所对的圆周角为直角;掌握四点共圆的判定方法和圆的内接四边形的性质;运用正方形的判定与性质以及同底等高的三角形的面积相等进行几何计算.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
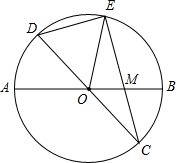 已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=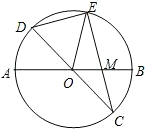 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.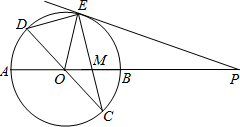 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=