题目内容
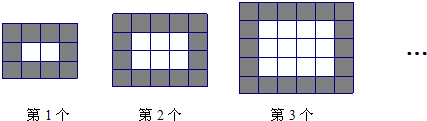
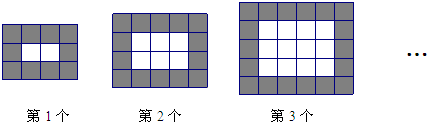
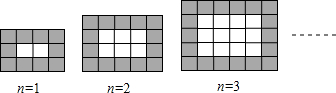
如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面.
(1)观察图形填写下列表格:
| 第n个图形 | 1 | 2 | 3 | … | n |
| 黑色小正方形个数 | 10 | … | |||
| 白色小正方形个数 | 1×2 | … |

解:(1)由题意,得
(2)依题意,得 4n+6+n(n+1)=506,
方程化为:n2+5n-500=0,
解得:n1=20,n2=-25(不合题意舍去).
∴4×(4n+6)+3n(n+1)
=4×(4×20+6)+3×20×(20+1)
=1604
∴一共需花1604元钱购买瓷砖.
分析:(1)由观察图形的变化规律可以得出白色小正方形的个数的变化规律,再由第n个图形的小正方形的个数-白色小正方形的个数就可以求出黑色小正方形的变化规律而得出结论;
(2)根据(1)的结论建立方程求出n的值,从而求出黑瓷砖与白瓷砖的数量,进而由总价=单价×数量可以得出结论.
点评:本题考查了规律型,图形的变化规律的运用,列一元二次方程解实际问题的运用,一元一次方程的解法的运用,解答时由图形变化求出黑色小正方形和白色小正方形的个数是关键.
| 第n个图形 | 1 | 2 | 3 | … | n |
| 黑色小正方形个数 | 10 | 14 | 18 | … | 4n+6 |
| 白色小正方形个数 | 1×2 | 2×3 | 3×4 | … | n(n+1) |
方程化为:n2+5n-500=0,
解得:n1=20,n2=-25(不合题意舍去).
∴4×(4n+6)+3n(n+1)
=4×(4×20+6)+3×20×(20+1)
=1604
∴一共需花1604元钱购买瓷砖.
分析:(1)由观察图形的变化规律可以得出白色小正方形的个数的变化规律,再由第n个图形的小正方形的个数-白色小正方形的个数就可以求出黑色小正方形的变化规律而得出结论;
(2)根据(1)的结论建立方程求出n的值,从而求出黑瓷砖与白瓷砖的数量,进而由总价=单价×数量可以得出结论.
点评:本题考查了规律型,图形的变化规律的运用,列一元二次方程解实际问题的运用,一元一次方程的解法的运用,解答时由图形变化求出黑色小正方形和白色小正方形的个数是关键.

练习册系列答案
相关题目