题目内容
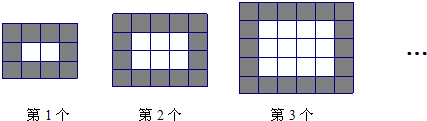
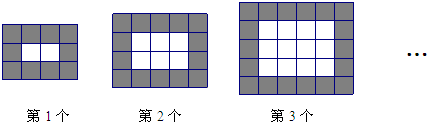
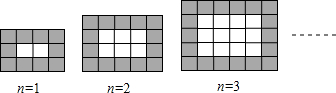
16、如图,用同样规格黑白两色的正方形瓷砖铺设地面,请观察右边图形并解答有关问题:
(1)在第n个图形中,需用白瓷砖
(2)按上述的铺设方案,设铺一块这样的矩形地面共用506块瓷砖,且黑瓷砖每块4元,白瓷砖每块3元,问一共需花多少元钱购买瓷砖?
(3)是否存在黑、白瓷砖块数相等的情形请通过计算说明理由.

(1)在第n个图形中,需用白瓷砖
n(n+1)
块,黑瓷砖(4n+6)
块.(均用含n的代数式表示);(2)按上述的铺设方案,设铺一块这样的矩形地面共用506块瓷砖,且黑瓷砖每块4元,白瓷砖每块3元,问一共需花多少元钱购买瓷砖?
(3)是否存在黑、白瓷砖块数相等的情形请通过计算说明理由.

分析:(1)根据第n个图形的白瓷砖的每行有(n+1)个,每列有n个,即可表示白瓷砖的数量,再让总数减去白瓷砖的数量即为黑瓷砖的数量;
(2)首先根据总数求得n的值,然后分别求出白瓷砖和黑瓷砖的数量,再进一步计算总价钱;
(3)根据(1)中的代数式列方程求解分析.
(2)首先根据总数求得n的值,然后分别求出白瓷砖和黑瓷砖的数量,再进一步计算总价钱;
(3)根据(1)中的代数式列方程求解分析.
解答:解:(1)在第n个图形中,需用白瓷砖n(n+1)块,黑瓷砖(4n+6)块;
(2)结合图形得(n+3)(n+2)=506,
解得n=20或n=-25(不合题意,应舍去),
当n=20时,有白瓷砖420块,黑瓷砖86块,
共需花费86×4+420×3=1604(元).
(3)根据题意得n(n+1)=4n+6,
n2-3n-6=0,
此时没有整数解,
所以不存在.
(2)结合图形得(n+3)(n+2)=506,
解得n=20或n=-25(不合题意,应舍去),
当n=20时,有白瓷砖420块,黑瓷砖86块,
共需花费86×4+420×3=1604(元).
(3)根据题意得n(n+1)=4n+6,
n2-3n-6=0,
此时没有整数解,
所以不存在.
点评:解决此题的关键是能够正确结合图形用代数式表示出黑、白瓷砖的数量,再根据题意列方程求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目