题目内容
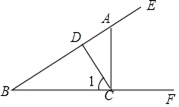
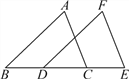
【题目】如图,△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm,点E与点C重合,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O在△ABC的重叠部分的面积为S(cm2). 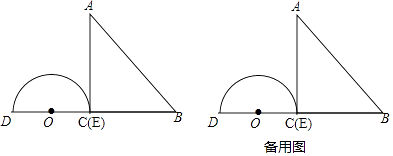
(1)当x=(s)时,点O与线段BC的中点重合;
(2)在(1)的条件下,求半圆O与△ABC的重叠部分的面积S;
(3)当x为何值时,半圆O所在的圆与△ABC的边所在的直线相切?
【答案】
(1)6
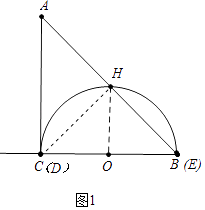
(2)解:如图1中,设⊙O与AB交于点H,连接OH,CH.
∵BC是直径,
∴∠CHB=90°,
∵AC=BC,∠ACB=90°,
∴∠HBC=∠HCB=45°,
∴HC=HB,
∴OH⊥BC,OH=OB=OC=6,
∴S=S扇形OHC+S△OHB= ![]() π62+
π62+ ![]() 66=18+9π
66=18+9π
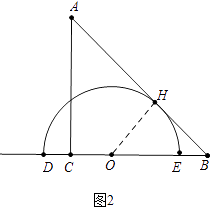
(3)解:如图2中,当⊙O与AB相切时(点O在点B左侧),易知OH=BH=6,OB=6 ![]() ,OC=12﹣6
,OC=12﹣6 ![]() ,
,
∴x= ![]() =9﹣3
=9﹣3 ![]() .
.
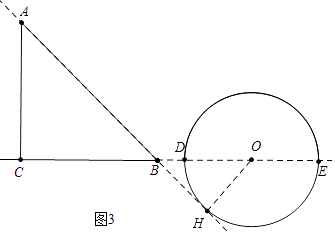
如图3中,当⊙O与AB相切时(点O在点B右侧),易知OH=BH=6,OB=6 ![]() ,OC=12+6
,OC=12+6 ![]() ,
,
∴x= ![]() =9+3
=9+3 ![]() .
.
如图1中,x=6时,⊙O与AC相切.
综上所述,当x=0或(9﹣3 ![]() )或6或(9+3
)或6或(9+3 ![]() )s时,半圆O所在的圆与△ABC的边所在的直线相切
)s时,半圆O所在的圆与△ABC的边所在的直线相切
【解析】解:(1)如图1中,当点O在AB的中点时,x= ![]() =6s.
=6s. 
所以答案是6s.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?