题目内容
(2003•十堰)先阅读下面的材料,再解答下面的各题.在平面直角坐标系中,有AB两点,A(x1,y1)、B(x2,y2)两点间的距离用|AB|表示,则有|AB|=
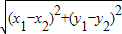 ,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|
,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2||BE|=|BD|-|DE|=|y2-y1|=||y1-y2|
在Rt△AEB中,由勾股定理得|AB|2=|AE|2+|BE|2=|x1-x2|2+|y1-y2|2
∴|AB|=
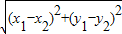 (因为|AB|表示线段长,为非负数)
(因为|AB|表示线段长,为非负数)注:当A、B在其它象限时,同理可证上述公式成立.
(1)在平面直角坐标系中有P(4,6)、Q(2,-3)两点,求|PQ|.
(2)如图2,直线L1与L2相交于点C(4,6),L1、L2与X轴分别交于B、A两点,其坐标B(8,0)、A(1,0),直线L3平行于X轴,与L1、L2分别交于E、D两点,且|DE|=
 ,求线段|DA|的长.
,求线段|DA|的长.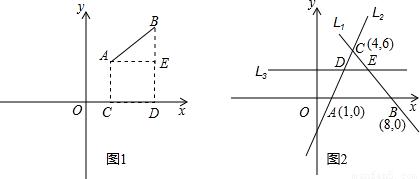
【答案】分析:(1)利用|PQ|= 即可求解;
即可求解;
(2)利用所给公式求出AC、AB的长度,结合相似三角形的性质对应边的比相等,即可求出CD的长,最后求出答案.
解答:解:(1)|PQ|=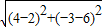 =
=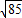 ;
;
(2)因为AC=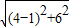 =3
=3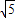 ,AB=8-1=7,直线L3平行于X轴,与L1、L2分别交于E、D两点,且|DE|=
,AB=8-1=7,直线L3平行于X轴,与L1、L2分别交于E、D两点,且|DE|= ,
,
所以△CDE∽△CAB.
所以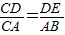 ,
,
即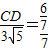 .
.
所以CD=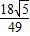 ,AD=
,AD=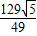 .
.
点评:本题需仔细分析题意,利用所给公式结合相似三角形的性质即可解决问题.
 即可求解;
即可求解;(2)利用所给公式求出AC、AB的长度,结合相似三角形的性质对应边的比相等,即可求出CD的长,最后求出答案.
解答:解:(1)|PQ|=
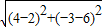 =
=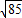 ;
;(2)因为AC=
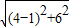 =3
=3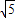 ,AB=8-1=7,直线L3平行于X轴,与L1、L2分别交于E、D两点,且|DE|=
,AB=8-1=7,直线L3平行于X轴,与L1、L2分别交于E、D两点,且|DE|= ,
,所以△CDE∽△CAB.
所以
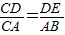 ,
,即
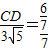 .
.所以CD=
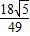 ,AD=
,AD=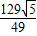 .
.点评:本题需仔细分析题意,利用所给公式结合相似三角形的性质即可解决问题.

练习册系列答案
相关题目
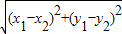 ,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|
,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|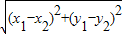 (因为|AB|表示线段长,为非负数)
(因为|AB|表示线段长,为非负数) ,求线段|DA|的长.
,求线段|DA|的长.