Question

【题目】.在△ABC中，，，直线经过点，且于， 于.

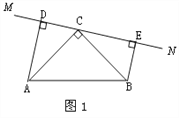
(1)当直线绕点旋转到图1的位置时， 的数量关系是_________________ ，并请给出证明过程.

(2)当直线绕点旋转到图2的位置时， 的数量关系是_________________ （直接写出结果）。

Answer 1

【答案】（1）DE=AD+BE，理由见解析；（2）DE=AD﹣BE

【解析】试题分析：（1）由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE，根据AAS可证明△ADC≌△CEB（AAS），依据全等三角形的性质可得到AD=CE，CD=BE，然后由ED=DC+CE可得到问题的答案；

（2）与（1）证法类似可证出∠ACD=∠EBC，能推出△ADC≌△CEB，得到AD=CE，CD=BE，最后由CE=CD+DE可得到问题的答案．

试题解析：证明：（1）∵AD⊥DE，BE⊥DE，∴∠ADC=∠BEC=90°．∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE．在△ADC和△CEB中∵∠CDA=∠BEC，∠DAC=∠ECB，AC=BC，∴△ADC≌△CEB（AAS），∴AD=CE，CD=BE，∵DC+CE=DE，∴AD+BE=DE．

（2）DE=AD﹣BE．理由：

∵BE⊥EC，AD⊥CE，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC，在△ADC和△CEB中，∵∠ACD=∠CBE，∠ADC=∠BEC，AC=BC，∴△ADC≌△CEB（AAS），∴AD=CE，CD=BE，∴DE=EC﹣CD=AD﹣BE．