题目内容
已知
,则
___ .
,则___ .4
假设m2+n2=y，得出关于y的一元二次方程，进而求出即可，注意平方数的性质．
解：假设m2+n2=y，
∵（m2+n2）（m2+n2-2）-8=0，
∴y（y-2）-8=0，
∴y2-2y-8=0，
∴（y-4）（y+2）=0，
∴y1=-2，y2=4，
∵m2+n2≥0，
∴m2+n2=4．
故答案为：4．
此题主要考查了换元法解一元二次方程以及因式分解法解一元二次方程，熟练应用因式分解法解一元二次方程可以降低计算量．
解：假设m2+n2=y，
∵（m2+n2）（m2+n2-2）-8=0，
∴y（y-2）-8=0，
∴y2-2y-8=0，
∴（y-4）（y+2）=0，
∴y1=-2，y2=4，
∵m2+n2≥0，
∴m2+n2=4．
故答案为：4．
此题主要考查了换元法解一元二次方程以及因式分解法解一元二次方程，熟练应用因式分解法解一元二次方程可以降低计算量．
练习册系列答案
相关题目
是一元二次方程，则
的解是 （ ）
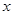的方程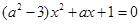
是一元二次方程的条件是 （ ）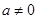
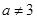
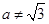
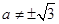
的解为
；则方程
=2009，
= ．
的值:
