题目内容
【题目】△ABC中,∠ACB=90°,AC=BC,直线l经过点C,BD⊥l,AE⊥l,,垂足分别为D、E.
(1)当A、B在直线l同侧时,如图1,
①证明:△AEC≌△CDB;
②若AE=3,BD=4,计算△ACB的面积.(提示:间接求)
(2)当A. B在直线l两侧时,如图2,若AE=3,BD=4,连接AD,BE直接写出梯形ADBE的面积___.

【答案】(1)①见解析;②12.5;(2)3.5
【解析】
(1)①根据垂直定义求出∠AEC=∠BDC=90°,求出∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,求出∠EAC=∠BCD,根据AAS推出△AEC≌△CDB;
②根据全等三角形的性质推出CE=BD和AE=CD即可,再利用勾股定理得出AC和BC的长计算即可;
(2)根据垂直定义求出∠AEC=∠BDC=90°,求出∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,求出∠EAC=∠BCD,根据AAS推出△AEC≌△CDB,根据全等三角形的性质推出CE=BD和AE=CD即可,利用梯形面积解答即可.
(1)①∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
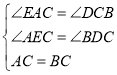 ,
,
∴△AEC≌△CDB(AAS);
②∵△AEC≌△CDB,
∴CE=BD,AE=CD,∠ACE=∠DBC,
∵ED=CE+CD,∠DBC+∠BCD=90°,
∴ED=AE+BD,∠ACE+∠BCD=90°,
在Rt△ACB中,AC=BC=![]() =5,
=5,
∴△ACB的面积=![]() ×5×5=12.5;
×5×5=12.5;
(2)∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
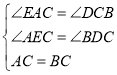 ,
,
∴△AEC≌△CDB(AAS),
∴CE=BD,AE=CD,
∵ED=CECD,
∴ED=BDAE=43=1,
梯形ADBE的面积=![]() ×(3+4)×1=3.5.
×(3+4)×1=3.5.
故答案为:3.5.

【题目】为庆祝国庆节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校分别单独购买服装,一共应付5000元.
(1)甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装共可以节省多少钱?