题目内容
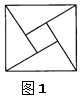
(1)如图1,请你将一张长方形的纸对折、再对折,然后按图中所示随意撕去一小部分,再将纸展开,把得到的图案画在试卷上,从对称的角度来说,你画出的这个图形有哪些几何特征?(2)如图2,已知△ABC.
①作∠B的角平分线;(要求:用尺规作图、保留作图痕迹,不写作法和证明)
②若∠C=90°,∠B=60°,BC=4,∠B的平分线交AC于D,请求出线段BD的长.

分析:(1)对折两次得到的图形既是中心对称图形,也是轴对称图形,折痕即是对称轴,所以说至少有两条对称轴;
(2)根据相应的三角函数值可得到所求的线段长.
(2)根据相应的三角函数值可得到所求的线段长.
解答: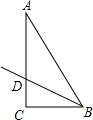 解:(1)画出的这个图形有以下的几何特征:是轴对称图形;是中心对称图形;至少两条对称轴;
解:(1)画出的这个图形有以下的几何特征:是轴对称图形;是中心对称图形;至少两条对称轴;
(2)∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=
∠ABC=30°,(5分)
∴Rt△BCD中,∠C=90°,
∴cos∠DBC=
,(6分)
∴BD=
=
=
=
.(7分)
 解:(1)画出的这个图形有以下的几何特征:是轴对称图形;是中心对称图形;至少两条对称轴;
解:(1)画出的这个图形有以下的几何特征:是轴对称图形;是中心对称图形;至少两条对称轴;(2)∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=
| 1 |
| 2 |
∴Rt△BCD中,∠C=90°,
∴cos∠DBC=
| BC |
| BD |
∴BD=
| BC |
| cos∠DBC |
| 4 |
| cos30° |
| 4 | ||||
|
8
| ||
| 3 |
点评:本题主要考查了剪纸得到图形的性质,以及在直角三角形中可利用三角函数来解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目