��Ŀ����
����Ŀ������������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1��x2+2x+2��y2��x2��2x+2�ǡ�����y��Գƶ��κ�������
��1��ֱ��д������ͼ�С�����y��Գƶ��κ�����ͼ�������еĹ�ͬ�ص㣮
��2�����κ���y��2��x+2��2+1�ġ�����y��Գƶ��κ���������ʽΪ�� �������κ���y��a��x��h��2+k�ġ�����y��Գƶ��κ���������ʽΪ�� ����
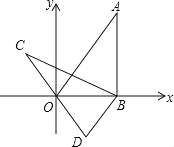
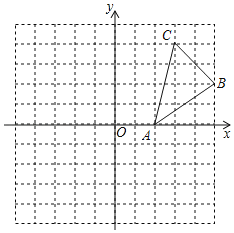
��3��ƽ��ֱ������ϵ�У��ǡ�����y��Գƶ��κ�������ͼ����y��Ľ���ΪA�����ǵ���������ֱ�ΪB��C����BC��6��˳�����ӵ�A��B��O��C�õ�һ�����Ϊ24�����Σ�����y��Գƶ��κ������ĺ�������ʽ��
���𰸡���1�������������2��y��2��x��2��2+1��y��a��x+h��2+k����3��y����![]() ��x��3��2��4��
��x��3��2��4��
��������
��1������������y��Գƶ��κ��������ɵô𰸣�
��2������������y��Գƶ��κ��������ɵô𰸣�
��3������������y��Գƶ��κ����������ε�������ɵö������꣬ͼ����y��Ľ��㣬���ݴ���ϵ�������ɵô𰸣�
�⣺��1��ֱ��д������ͼ�С�����y��Գƶ��κ�����ͼ�������еĹ�ͬ�ص�ʱ�������y��Գƣ��Գ������y��Գƣ�
��2�����κ���y��2��x+2��2+1�ġ�����y��Գƶ��κ���������ʽΪ y��2��x��2��2+1��
���κ���y��a��x��h��2+k�ġ�����y��Գƶ��κ���������ʽΪy��a��x+h��2+k��
�ʴ�Ϊ��y��2��x��2��2+1��y��a��x+h��2+k��
��3����ͼ��

��BC��6��˳�����ӵ�A��B��O��C�õ�һ�����Ϊ24�����Σ���
OA��8��A��������0��8����B�����������3��4����
��һ�������ߵĽ���ʽΪy��a��x+3��2+4����A��������룬��
9a+4��8��
���a��![]() ��
��
y��![]() ��x+3��2+4����y��Գƶ��κ����ĺ�������ʽy��
��x+3��2+4����y��Գƶ��κ����ĺ�������ʽy��![]() ��x��3��2+4��
��x��3��2+4��
���ݶԳ��ԣ��������µ�������Ҳ�������⣬
������y��Գƶ��κ������ĺ�������ʽΪy����![]() ��x+3��2��4����y��Գƶ��κ����ĺ�������ʽy����
��x+3��2��4����y��Գƶ��κ����ĺ�������ʽy����![]() ��x��3��2��4��
��x��3��2��4��

 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�