题目内容
【题目】阅读理解:在平面直角坐标系中,任意两点A(x1,y1),B(x2,y2)之间的位置关系有以下三种情形;
①如果AB∥x轴,则y1=y2,AB=|x1﹣x2|
②如果AB∥y轴,则x1=x2,AB=|y1﹣y2|
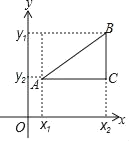
③如果AB与x轴、y轴均不平行,如图,过点A作与x轴的平行线与过点B作与y轴的平行线相交于点C,则点C坐标为(x2,y1),由①得AC=|x1﹣x2|;由②得BC=|y1﹣y2|;根据勾股定理可得平面直角坐标系中任意两点的距离公式AB=![]() .
.
小试牛刀:
(1)若点A坐标为(﹣2,3),B点坐标为(3,3)则AB= ;
(2)若点A坐标为(3,2),B点坐标为(3,﹣4)则AB= ;
(3)若点A坐标为(3,2),B点坐标为(7,﹣1)则AB= ;
学以致用:
若点A坐标为(2,2),点B坐标为(4,4),点P是x轴上的动点,当AP+PB取得最小值时点P的坐标为 并求出AP+PB最小值= ;
挑战自我:
已知M=![]() ,N=
,N=![]() 根据数形结合,直接写出M的最小值= ;N的最大值= ;
根据数形结合,直接写出M的最小值= ;N的最大值= ;
【答案】小试牛刀:(1)5;(2)6;(3)5;学以致用:(![]() ,0),2
,0),2![]() ;挑战自我: 3
;挑战自我: 3![]() ;2
;2![]() .
.
【解析】
小试牛刀:(1)利用两点间的距离公式AB=|x1-x2|进行解答;
(2)利用两点间的距离公式AB=|y1-y2|进行解答;
(3)利用两点间的距离公式AB=![]() 进行解答;
进行解答;
学以致用:利用轴对称的性质求得点P的坐标以及AP+PB的最小值;
挑战自我:利用M、N所表示的几何意义解答.
小试牛刀:(1)AB=|x1﹣x2|=|3﹣(﹣2)|=5.
(2)AB=|y1﹣y2|=|﹣4﹣2|=6.
(3)AB=![]() =
=![]() =5.
=5.
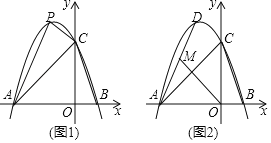
学以致用:如图,
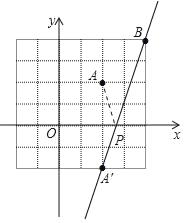
∵点A坐标为(2,2),
∴点A关于x轴对称的点A′的坐标是(2,﹣2),
连接A′B,直线A′B与x轴的交点即为点P.
设直线A′B为y=kx+b(k≠0),则![]() ,
,
解得![]() .
.
∴直线A′B为y=3x﹣8.
令y=0,则x=![]() ,
,
即P(![]() ,0),
,0),
此时AP+PB=A′B=![]() .
.
挑战自我:M=![]() ,
,
当M取最小值时,M表示点(x,0)与点(6,4)的距离与点(x,0)与点 (3,2)的距离之和(或M表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,﹣2)的距离之和),
此时M最小值=![]() .
.
N=![]() ,
,
当N取最大值时,N表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,﹣4)的距离与点(x,0)与点 (3,2)的距离之差),
此时M最小值=![]() .
.