题目内容
已知:抛物线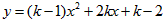 与x轴有两个不同的交点。
与x轴有两个不同的交点。
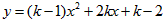 与x轴有两个不同的交点。
与x轴有两个不同的交点。
(1)求k的取值范围;
(2)当k为整数,且关于x的方程3x=kx-1的解是负数时,求抛物线的解析式;
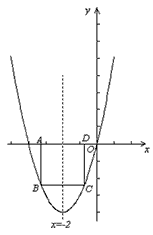
(3)在(2)的条件下,若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长。
(2)当k为整数,且关于x的方程3x=kx-1的解是负数时,求抛物线的解析式;
(3)在(2)的条件下,若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长。
|
解:(1) |
 |

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
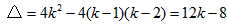 ,
,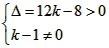 ,
,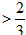 且k≠1,①;
且k≠1,①; ,
,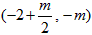 ,
,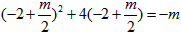 ,
,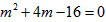 ,
,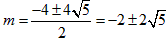 (舍负),
(舍负), 。
。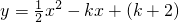 与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
与x轴正半轴交于A、B两点(A点在B点左边),且AB=4. 交于C、D两点,求S△ACD;
交于C、D两点,求S△ACD;