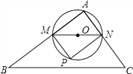
题目内容
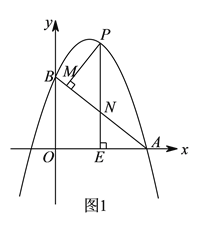
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上的动点(不与
上的动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]()
于点![]() .以
.以![]() 为直径作
为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() ,令
,令![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ;
;
![]() 当
当![]() 为何值时,
为何值时,![]() 与直线
与直线![]() 相切?
相切?
【答案】![]() .
.![]() 当
当![]() 时,
时,![]() 与
与![]() 相切.
相切.
【解析】(1)由△AMN∽△ABC得出AN,又S△AMN=S△MNP,求得△AMN的面积即可.
(2)设直线BC与⊙O相切于点D,连接AO,OD,并过点M作MQ⊥BC于Q,由(1)中△AMN∽△ABC得![]() ,则求得MN、OD,再证△BMQ∽△BCA,得
,则求得MN、OD,再证△BMQ∽△BCA,得![]() ,代入求得x的值.
,代入求得x的值.
![]() ∵
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() .
.![]()
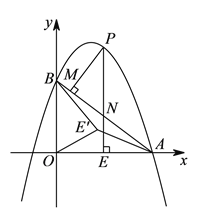
(2)如图,设直线BC与⊙O相切于点D,连接AO,OD.
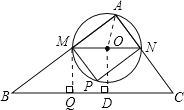
![]() .
.
在![]() 中,
中,![]() .
.
由![]() 知
知![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() .
.
过点![]() 作
作![]() 于
于![]() ,则
,则![]() .
.
在![]() 与
与![]() 中,
中,![]() 是公共角,
是公共角,
∴![]() .
.
∴![]() ,即
,即![]() .
.
解得![]() .
.
![]() .
.
解得![]() ,即当
,即当![]() 时,
时,![]() 与
与![]() 相切.
相切.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目