题目内容
(2012•武侯区一模)(1)计算:(-1)2012-|1-6tan30°|-(-
)0+
;
(2)解方程组:
;
(3)先化简,再求值:
÷
-
,其中x=-
,y=-1.
| 5 |
| 12 |
(2)解方程组:
|
(3)先化简,再求值:
| x-y |
| x+3y |
| x2-y2 |
| x2+6xy+9y2 |
| 3y |
| x+y |
| 1 |
| 2 |
分析:(1)先根据整数指数幂,绝对值、特殊角的三角函数值、零指数幂等知识点分别进行计算,再合并即可求出答案;
(2)根据解方程的步骤,先消去y,求出x的值,再把x的值代入即可求出y的值;
(3)先把除法转化成乘法,再进行约分,然后把x,y的值代入即可求出答案.
(2)根据解方程的步骤,先消去y,求出x的值,再把x的值代入即可求出y的值;
(3)先把除法转化成乘法,再进行约分,然后把x,y的值代入即可求出答案.
解答:解:(1)(-1)2012-|1-6tan30°|-(-
)0+
=1-(2
-1)-1+2
=1;
(2)
,
由①×2得:4x-2y=-10,③,
③+②得:7x=-14,
x=-2,
把x=-2代入①得:y=1,
所以方程组的解是
.
(3)
÷
-
=
×
-
=
-
=
,
把x=-
,y=-1代入上式得:
=
.
| 5 |
| 12 |
=1-(2
| 3 |
| 3 |
=1;
(2)
|
由①×2得:4x-2y=-10,③,
③+②得:7x=-14,
x=-2,
把x=-2代入①得:y=1,
所以方程组的解是
|
(3)
| x-y |
| x+3y |
| x2-y2 |
| x2+6xy+9y2 |
| 3y |
| x+y |
=
| x-y |
| x+3y |
| (x+3y)2 |
| (x+y)(x-y) |
| 3y |
| x+y |
=
| x+3y |
| x+y |
| 3y |
| x+y |
=
| x |
| x+y |
把x=-
| 1 |
| 2 |
-
| ||
-
|
| 1 |
| 3 |
点评:此题考查了分式的化简求值,是各地中考题中常见的计算题型,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握零指数幂、整数指数幂、绝对值等概念.

练习册系列答案
相关题目
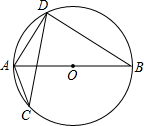 (2012•武侯区一模)如图,⊙O的弦CD与直径AB相交,若∠ACD=35°,则∠BAD=( )
(2012•武侯区一模)如图,⊙O的弦CD与直径AB相交,若∠ACD=35°,则∠BAD=( )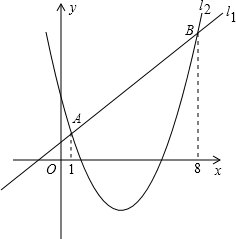 (2012•武侯区一模)如图,直线
(2012•武侯区一模)如图,直线