Question

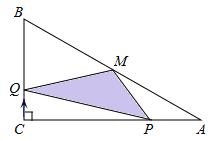
【题目】如图，在平面直角坐标系中，直线y＝﹣5x+5与x轴、y轴分别交于A，C两点，抛物线y＝x2+bx+c经过A，C两点，与x轴交于另一点B．

（1）求抛物线解析式及B点坐标；

（2）x2+bx+c≤﹣5x+5的解集是　 　；

（3）若点M为抛物线上一动点，连接MA、MB，当点M运动到某一位置时，△ABM面积为△ABC的面积的倍，求此时点M的坐标．

Answer 1

【答案】（1）（5，0）；（2）0≤x≤1；（3）（3，﹣4）或（3+2，4）或（3﹣2，4）

【解析】

（1）根据已知条件将A点、C点代入抛物线即可求解；

（2）观察直线在抛物线上方的部分，根据抛物线与直线的交点坐标即可求解；

（3）先设动点M的坐标，再根据两个三角形的面积关系即可求解．

（1）因为直线y＝﹣5x+5与x轴、y轴分别交于A，C两点，

所以当x＝0时，y＝5，所以C（0，5）

当y＝0时，x＝1，所以A（1，0）

因为抛物线y＝x2+bx+c经过A，C两点，

所以c＝5，1+b+5＝0，解得b＝﹣6，

所以抛物线解析式为y＝x2﹣6x+5．

当y＝0时，0＝x2﹣6x+5．解得x1＝1，x2＝5．

所以B点坐标为（5，0）．

答：抛物线解析式为y＝x2﹣6x+5，B点坐标为（5，0）；

（2）观察图象可知：

x2+bx+c≤﹣5x+5的解集是0≤x≤1．

故答案为0≤x≤1．

（3）设M（m，m2﹣6m+5）

因为S△ABM＝S△ABC＝×4×5＝8．

所以×4|m2﹣6m+5|＝8

所以|m2﹣6m+5|＝±4．

所以m2﹣6m+9＝0或m2﹣6m+1＝0

解得m1＝m2＝3或m＝3±2．

所以M点的坐标为（3，﹣4）或（3+2，4）或（3﹣2，4）．

答：此时点M的坐标为（3，﹣4）或（3+2，4）或（3﹣2，4）．