题目内容
如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
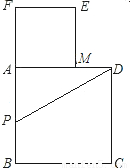
【答案】分析:(1)要求AM的长,只需求得AF的长,又AF=PF-AP,PF=PD=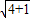 =
=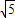 ,则AM=AF=
,则AM=AF=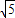 -1,DM=AD-AM=3-
-1,DM=AD-AM=3- ;
;
(2)根据(1)中的数据得: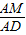 =
=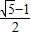 ,根据黄金分割点的概念,则点M是AD的黄金分割点.
,根据黄金分割点的概念,则点M是AD的黄金分割点.
解答:解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD= =
=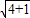 =
=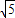 ,
,
∴AM=AF=PF-AP=PD-AP=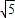 -1,
-1,
DM=AD-AM=3- .
.
故AM的长为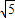 -1,DM的长为3-
-1,DM的长为3-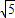 ;
;
(2)点M是AD的黄金分割点.
由于 =
= ,
,
∴点M是AD的黄金分割点.
点评:此题综合考查了正方形的性质、勾股定理和黄金分割的概念.先求得线段AM,DM的长,然后求得线段AM和AD,DM和AM之间的比,根据黄金分割的概念进行判断.
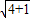 =
=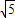 ,则AM=AF=
,则AM=AF=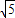 -1,DM=AD-AM=3-
-1,DM=AD-AM=3- ;
;(2)根据(1)中的数据得:
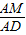 =
=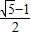 ,根据黄金分割点的概念,则点M是AD的黄金分割点.
,根据黄金分割点的概念,则点M是AD的黄金分割点.解答:解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD=
 =
=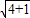 =
=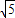 ,
,∴AM=AF=PF-AP=PD-AP=
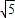 -1,
-1,DM=AD-AM=3-
 .
.故AM的长为
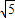 -1,DM的长为3-
-1,DM的长为3-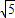 ;
;(2)点M是AD的黄金分割点.
由于
 =
= ,
,∴点M是AD的黄金分割点.
点评:此题综合考查了正方形的性质、勾股定理和黄金分割的概念.先求得线段AM,DM的长,然后求得线段AM和AD,DM和AM之间的比,根据黄金分割的概念进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
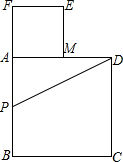 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,
如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
A、
| ||||
B、
| ||||
C、3-
| ||||
D、6-2
|
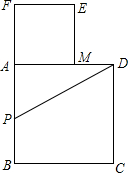 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.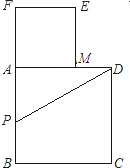 如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.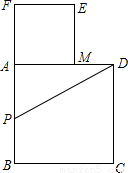 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.