题目内容
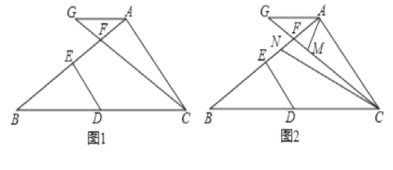
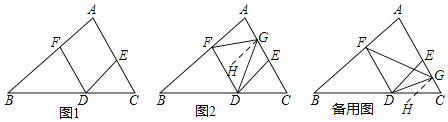
【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.
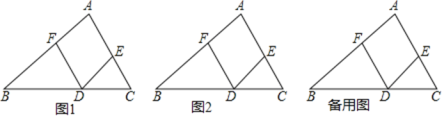
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)依据DE∥AB,DF∥AC,可得∠EDF+∠AFD=180°,∠A+∠AFD=180°,进而得出∠EDF=∠A;
(2)①过G作GH∥AB,依据平行线的性质,即可得到∠AFG+∠EDG=∠FGH+∠DGH=∠DGF;②过G作GH∥AB,依据平行线的性质,即可得到∠AFG-∠EDG=∠FGH-∠DGH=∠DGF.
解:(1)∵DE∥AB,DF∥AC,
∴∠EDF+∠AFD=180°,∠A+∠AFD=180°,
∴∠EDF=∠A;
(2)①∠AFG+∠EDG=∠DGF.
如图2所示,过G作GH∥AB,
∵AB∥DE,
∴GH∥DE,
∴∠AFG=∠FGH,∠EDG=∠DGH,
∴∠AFG+∠EDG=∠FGH+∠DGH=∠DGF;
②∠AFG-∠EDG=∠DGF.
如图所示,过G作GH∥AB,
∵AB∥DE,
∴GH∥DE,
∴∠AFG=∠FGH,∠EDG=∠DGH,
∴∠AFG-∠EDG=∠FGH-∠DGH=∠DGF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】现有两个可以自由转动的转盘,每个转盘分成三个相同的扇形,涂色情况如图所示,指针的位置固定,同时转动两个转盘,回答以下问题:

圆1 圆2
圆2 圆1 | |||
(1)补全表格:圆1的所有可能结果有 种,分别是 ;
圆2的所有可能结果有 种,分别是 .
(2)写出:转盘停止后指针指向同种颜色区域的概率和至少有一指针指向红色区域的概率.