题目内容
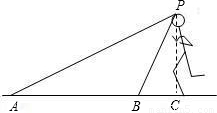
在08北京奥运会上,百米飞人博尔特以9.69s的成绩打破世界纪录并轻松夺冠.A、B两镜头同时拍下了博尔特冲刺时的画面(如图),从B镜头观测到博尔特的仰角为60°,从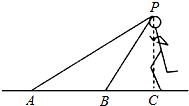 镜头A观测到博尔特的仰角为30°,若冲刺时的头顶P到地面的距离PC大约为1.95m,请计算A、B两镜头当时所在位置之间的距离.(
镜头A观测到博尔特的仰角为30°,若冲刺时的头顶P到地面的距离PC大约为1.95m,请计算A、B两镜头当时所在位置之间的距离.( ≈1.732,结果保留两位小数)
≈1.732,结果保留两位小数)
解:在Rt△BPC中,
∵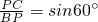
∴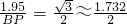
∴BP≈2.25m;
∵∠PAB=30°,∠PBC=60°,
∴∠APB=30°,
∴AB=BP≈2.25m.
答:A、B两镜头当时所在位置的距离为2.25米.
分析:首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
点评:本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
∵
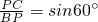
∴
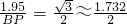
∴BP≈2.25m;
∵∠PAB=30°,∠PBC=60°,
∴∠APB=30°,
∴AB=BP≈2.25m.
答:A、B两镜头当时所在位置的距离为2.25米.
分析:首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
点评:本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
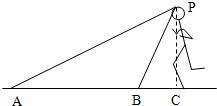
 镜头A观测到博尔特的仰角为30°,若冲刺时的头顶P到地面的距离PC大约为1.95m,请计算A、B两镜头当时所在位置之间的距离.(
镜头A观测到博尔特的仰角为30°,若冲刺时的头顶P到地面的距离PC大约为1.95m,请计算A、B两镜头当时所在位置之间的距离.(