题目内容
 31、如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;
31、如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;由此验证了乘法公式:
(a-b)2=a2-2ab+b2
.分析:由于空白正方形的边长为(a-b),长方形的长为(a-b),宽为b,利用面积的割补法即可得到完全平方公式的形式.
解答:解:空白正方形的边长为(a-b),长方形的长为(a-b),宽为b,
第一种方法得空白正方形面积=(a-b)2,
第一种方法得空白正方形面积=a2-2(a-b)b-b2=a2-2ab+b2,
∴(a-b)2=a2-2ab+b2.
故答案为:(a-b)2=a2-2ab+b2.
第一种方法得空白正方形面积=(a-b)2,
第一种方法得空白正方形面积=a2-2(a-b)b-b2=a2-2ab+b2,
∴(a-b)2=a2-2ab+b2.
故答案为:(a-b)2=a2-2ab+b2.
点评:此题主要考查了完全平方公式的几何背景,解题的关键是会利用面积的割补法得到公式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
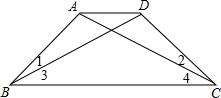
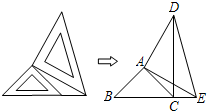
 21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:
21、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.求证:
 如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;由此验证了乘法公式:________.
如图是由两个大小不同的正方形与两个全等的长方形拼成的一个大正方形,请用两种不同的方法表示图中空白正方形的面积;由此验证了乘法公式:________.