题目内容
三人相互传球，由甲开始发球，并作为第一次传球．
（1）用列表或画树状图的方法求经过3次传球后，球仍回到甲手中的概率是多少？
（2）由（1）进一步探索：经过4次传球后，球仍回到甲手中的不同传球的方法共有多少种？
（3）就传球次数n与球分别回到甲、乙、丙手中的可能性大小，提出你的猜想（写出结论即可）．
解：（1）画树状图得：
．
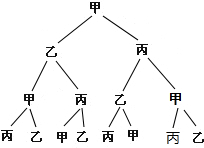经过三次传球后，球仍回到甲手中的概率P（球回到甲手中）P=
；
（2）
列表或画树状图正确．
经过4次传球后，球仍回到甲手中的不同传球的方法共有6种；
（3）猜想：当n为奇数时，P（球回到甲手中）＜P（球回到乙手中）=P（球回到丙手中）
当n为偶数时，P（球回到甲手中）＞P（球回到乙手中）=P（球回到丙手中）
（若解答中出现P（球回到乙手中）=P（球回到丙手中），则可得1分）．
分析：列举出所有情况，看所求的情况占总情况的多少即可．
点评：树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
．经过三次传球后，球仍回到甲手中的概率P（球回到甲手中）P=
；（2）
列表或画树状图正确．
经过4次传球后，球仍回到甲手中的不同传球的方法共有6种；
（3）猜想：当n为奇数时，P（球回到甲手中）＜P（球回到乙手中）=P（球回到丙手中）
当n为偶数时，P（球回到甲手中）＞P（球回到乙手中）=P（球回到丙手中）
（若解答中出现P（球回到乙手中）=P（球回到丙手中），则可得1分）．
分析：列举出所有情况，看所求的情况占总情况的多少即可．
点评：树状图法适用于两步或两步以上完成的事件；解题时还要注意是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
与球分别回到甲、乙、丙手中的可能性大小，提出你的猜想（写出结论即可）。（改编）