题目内容
【题目】把正整数1，2，3，4，…，2 009排列成如图所示的一个表．
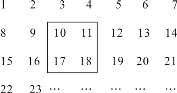
(1)用一正方形在表中随意框住4个数，把其中最小的数记为x，另三个数用含x的式子表示出来，从小到大依次是__ __，__ __，__ __；
(2)在(1)前提下，当被框住的4个数之和等于416时，x的值是多少？
(3)在(1)前提下，被框住的4个数之和能否等于622？如果能，请求出此时x的值；如果不能，请说明理由．
【答案】（1）x+1，x+7，x+8（2）x=100（3）详见解析
【解析】
从表格可看出框的4个数，左右相邻的差1，上下相邻的差7，设最小的数是x，右边的就为x+1，x下面的就为x+7，x+7右边的为x+8；把这四个数加起来和为416构成一元一次方程，可以解得x；加起来看看四个数为622时是否为整数，整数就可以，否则不行．
(1)用一正方形在表中随意框住4个数，把其中最小的数记为x，另三个数用含x的式子表示出来，从小到大依次是__x＋1__，__ x＋7__，__x＋8__；
(2)x＋(x＋1)＋(x＋7)＋(x＋8)＝416，
4x＋16＝416，解得x＝100.
(3)被框住的4个数之和不可能等于622.理由：
∵x＋(x＋1)＋(x＋7)＋(x＋8)＝622，
∴4x＋16＝622，x＝151.5，
∵x是正整数，不可能是151.5，
∴被框住的4个数之和不可能等于622.
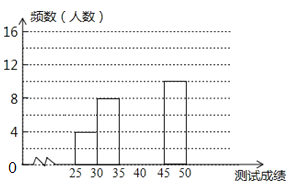
【题目】为了提高学生书写汉字的能力．增强保护汉字的意识，我区举办了“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 25≤x＜30 | 4 |
第2组 | 30≤x＜35 | 6 |
第3组 | 35≤x＜40 | 14 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
请结合图表完成下列各题：
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
