题目内容
 (2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,
(2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,| 1 |
| 4 |
(1)求抛物线C1的解析式的一般形式;
(2)当m=2时,求h的值;
(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF-tan∠ECP=
| 1 |
| 2 |
分析:(1)设抛物线C1的顶点式形式y=a(x-1)2,(a≠0),然后把点(0,
)代入求出a的值,再化为一般形式即可;
(2)先根据m的值求出直线AB与x轴的距离,从而得到点B、C的纵坐标,然后利用抛物线解析式求出点C的横坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相同求出点A的坐标,然后根据平移的性质设出抛物线C2的解析式,再把点A的坐标代入求出h的值即可;
(3)先把直线AB与x轴的距离是m2代入抛物线C1的解析式求出C的坐标,从而求出CE,再表示出点A的坐标,根据抛物线的对称性表示出ED,根据平移的性质设出抛物线C2的解析式,把点A的坐标代入求出h的值,然后表示出EF,最后根据锐角的正切值等于对边比邻边列式整理即可得证.
| 1 |
| 4 |
(2)先根据m的值求出直线AB与x轴的距离,从而得到点B、C的纵坐标,然后利用抛物线解析式求出点C的横坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相同求出点A的坐标,然后根据平移的性质设出抛物线C2的解析式,再把点A的坐标代入求出h的值即可;
(3)先把直线AB与x轴的距离是m2代入抛物线C1的解析式求出C的坐标,从而求出CE,再表示出点A的坐标,根据抛物线的对称性表示出ED,根据平移的性质设出抛物线C2的解析式,把点A的坐标代入求出h的值,然后表示出EF,最后根据锐角的正切值等于对边比邻边列式整理即可得证.
解答:(1)解:设抛物线C1的顶点式形式y=a(x-1)2,(a≠0),
∵抛物线过点(0,
),
∴a(0-1)2=
,
解得a=
,
∴抛物线C1的解析式为y=
(x-1)2,
一般形式为y=
x2-
x+
;
(2)解:当m=2时,m2=4,
∵BC∥x轴,
∴点B、C的纵坐标为4,
∴
(x-1)2=4,
解得x1=5,x2=-3,
∴点B(-3,4),C(5,4),
∵点A、C关于y轴对称,
∴点A的坐标为(-5,4),
设抛物线C2的解析式为y=
(x-1)2-h,
则
(-5-1)2-h=4,
解得h=5;
(3)证明:∵直线AB与x轴的距离是m2,
∴点B、C的纵坐标为m2,
∴
(x-1)2=m2,
解得x1=1+2m,x2=1-2m,
∴点C的坐标为(1+2m,m2),
又∵抛物线C1的对称轴为直线x=1,
∴CE=1+2m-1=2m,
∵点A、C关于y轴对称,
∴点A的坐标为(-1-2m,m2),
∴AE=ED=1-(-1-2m)=2+2m,
设抛物线C2的解析式为y=
(x-1)2-h,
则
(-1-2m-1)2-h=m2,
解得h=2m+1,
∴EF=h+m2=m2+2m+1,
∴tan∠EDF-tan∠ECP=
-
=
-
=
-
=
,
∴tan∠EDF-tan∠ECP=
.
∵抛物线过点(0,
| 1 |
| 4 |
∴a(0-1)2=
| 1 |
| 4 |
解得a=
| 1 |
| 4 |
∴抛物线C1的解析式为y=
| 1 |
| 4 |
一般形式为y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)解:当m=2时,m2=4,
∵BC∥x轴,
∴点B、C的纵坐标为4,
∴
| 1 |
| 4 |
解得x1=5,x2=-3,
∴点B(-3,4),C(5,4),
∵点A、C关于y轴对称,
∴点A的坐标为(-5,4),
设抛物线C2的解析式为y=
| 1 |
| 4 |
则
| 1 |
| 4 |
解得h=5;
(3)证明:∵直线AB与x轴的距离是m2,
∴点B、C的纵坐标为m2,
∴
| 1 |
| 4 |
解得x1=1+2m,x2=1-2m,
∴点C的坐标为(1+2m,m2),
又∵抛物线C1的对称轴为直线x=1,
∴CE=1+2m-1=2m,
∵点A、C关于y轴对称,
∴点A的坐标为(-1-2m,m2),
∴AE=ED=1-(-1-2m)=2+2m,
设抛物线C2的解析式为y=
| 1 |
| 4 |
则
| 1 |
| 4 |
解得h=2m+1,
∴EF=h+m2=m2+2m+1,
∴tan∠EDF-tan∠ECP=
| EF |
| ED |
| EP |
| CE |
| m2+2m+1 |
| 2+2m |
| m2 |
| 2m |
| m+1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
∴tan∠EDF-tan∠ECP=
| 1 |
| 2 |
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,二次函数图象与结合变换,关于y轴对称的点的坐标特征,抛物线上点的坐标特征,锐角的正切的定义,(3)用m表示出相应的线段是解题的关键,也是本题的难点.

练习册系列答案
相关题目
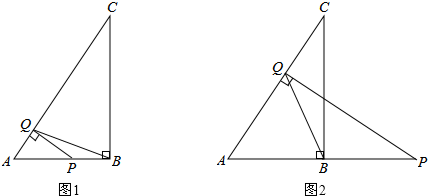
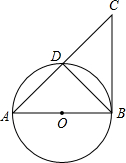 (2013•株洲)已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.
(2013•株洲)已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.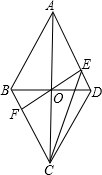 (2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.