题目内容
 (2013•龙岗区模拟)在矩形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F,若G是EF的中点,则∠BDG的正切值为
(2013•龙岗区模拟)在矩形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F,若G是EF的中点,则∠BDG的正切值为1
1
.分析:根据矩形性质得出∠BAD=∠DCB=∠ABE=90°,AB=DC,AD∥BC,求出DC=BE=AB,求出DF=BC,∠F=45°,求出CG=GF,证△DGF≌△BGC,推出∠BDG=∠F=45°,即可求出答案.
解答: 解:连接CG,BG,
解:连接CG,BG,
∵四边形ABCD是矩形,
∴∠BAD=∠DCB=∠ABE=90°,AB=DC,AD∥BC,
∵AE平分∠DAB,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°=∠BAE,
∵AB∥DC,
∴∠F=∠BAE=45°,
∴∠F=∠CEF,
∴CE=CF,
∵BE=DC,
∴DF=BC,
∵∠ECF=90°,CE=CF,G为EF中点,
∴∠ECG=45°,CG=GE=GF,
∴∠ECG=∠F,
在△DGF和△BGC中
∴△DGF≌△BGC,
∴∠BDG=∠F=45°,
∴∠BDG的正切值为tan45°=1,
故答案为:1.
 解:连接CG,BG,
解:连接CG,BG,∵四边形ABCD是矩形,
∴∠BAD=∠DCB=∠ABE=90°,AB=DC,AD∥BC,
∵AE平分∠DAB,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°=∠BAE,
∵AB∥DC,
∴∠F=∠BAE=45°,
∴∠F=∠CEF,
∴CE=CF,
∵BE=DC,
∴DF=BC,
∵∠ECF=90°,CE=CF,G为EF中点,
∴∠ECG=45°,CG=GE=GF,
∴∠ECG=∠F,
在△DGF和△BGC中
|
∴△DGF≌△BGC,
∴∠BDG=∠F=45°,
∴∠BDG的正切值为tan45°=1,
故答案为:1.
点评:本题考查了矩形的性质,全等三角形的性质和判定,等腰三角形的性质和判定,直角三角形斜边上中线性质的应用,综合性比较强,难度偏大.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
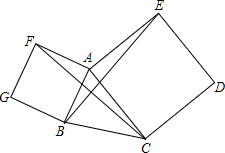 (2013•龙岗区模拟)如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
(2013•龙岗区模拟)如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.