题目内容
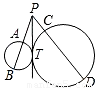
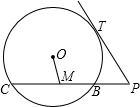如图，PT是⊙O的切线，切点是T，M是⊙O内一点，PM及PM的延长线交⊙O于B，C，BM=BP=2，PT=2| 5 |
分析：已知了PT、BP的长，根据切割线定理易求得BC的长；在线段OM的基础上作⊙O的直径，根据相交弦定理即可求出⊙O的半径．
解答：解：∵PT是⊙O的切线，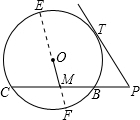
由切割线定理，得：PT2=PB•PC；
∵PT=2
，BP=2；
∴PC=PT2÷PC=10；
∴BC=8，CM=6；
过O、M作⊙O的直径，交⊙O于E、F；
设⊙O的半径为R，则EM=R+3，MF=R-3；
由相交弦定理，得：（R+3）（R-3）=BM•MC；
R2-9=2×6，即R=
．
故⊙O的半径为
．
由切割线定理，得：PT2=PB•PC；
∵PT=2
| 5 |
∴PC=PT2÷PC=10；
∴BC=8，CM=6；
过O、M作⊙O的直径，交⊙O于E、F；
设⊙O的半径为R，则EM=R+3，MF=R-3；
由相交弦定理，得：（R+3）（R-3）=BM•MC；
R2-9=2×6，即R=
| 21 |
故⊙O的半径为
| 21 |
点评：此题综合考查了切割线定理和相交弦定理．
练习册系列答案
相关题目
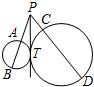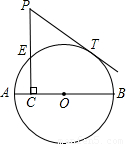
8、如图，PT是外切两圆的公切线，T为切点，PAB，PCD分别为这两圆的割线．若PA=3，PB=6，PC=2，则PD等于（ ）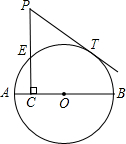
如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．
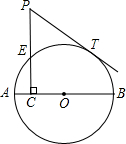如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．
