题目内容
在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )A.sinA=

B.cosA=

C.tanA=

D.cotA=

【答案】分析:根据三边长度判断三角形的形状;利用锐角三角函数的定义求解.
解答:解:在△ABC中,已知AC=3,BC=4,AB=5,
则△ABC是直角三角形,且AB是斜边.
因而sinA= ,
,
cosA=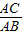 =
= ,
,
tanA=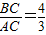 ,
,
cotA=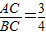 .
.
所以,结论成立的是cosA= .
.
故选B.
点评:本题重点考查了三角函数的定义,是需要识记的内容.
解答:解:在△ABC中,已知AC=3,BC=4,AB=5,
则△ABC是直角三角形,且AB是斜边.
因而sinA=
 ,
,cosA=
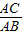 =
= ,
,tanA=
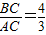 ,
,cotA=
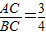 .
.所以,结论成立的是cosA=
 .
.故选B.
点评:本题重点考查了三角函数的定义,是需要识记的内容.

练习册系列答案
相关题目
