题目内容
若一个多边形的外角和是它的内角和的| 1 | 4 |
分析:多边形的外角和是360度,外角和是它的内角和的
,则内角和是1440度.n边形的内角和是(n-2)•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.
| 1 |
| 4 |
解答:解:根据题意,得
(n-2)•180=1440,
解得:n=10.
则此多边形的边数是10.
(n-2)•180=1440,
解得:n=10.
则此多边形的边数是10.
点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.

练习册系列答案
相关题目
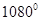 ,则这个多边形为 边形;
,则这个多边形为 边形;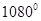 ,则这个多边形为 边形;
,则这个多边形为 边形;