题目内容
已知:如图,△ABC中,AB=BC=CA=6,BC在x轴上,BC边上的高线AO在y轴上,直线△APC点转动(与线段BC没有交点).设与AB、l、x轴相切的⊙O1的半径为r1,与AC、l、x轴相切的⊙O2的半径为r2(1)当直线l绕点A转到任何位置时,⊙O1、⊙O2的面积之和最小,为什么?
(2)若r1-r2=
| 3 |
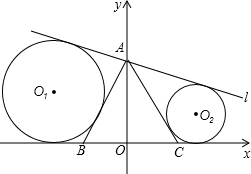
分析:(1)设切点分别为M、N、D、G.由切线长定理得MN+DG=AB+BC+AC=18,DB+CG=3.连接O1D、O1B,可求得DB=
r1.同理CG=
r2,则r1+r2=3
.⊙O1、⊙O2的面积之和S=πr12+π(3
-r1)2=2π[(r1-
)2+
].当r1=r2=
,即l∥x轴时,S最小;
(2)由(1)得r1+r2=3
,结合r1-r2=
,∠BDH=∠ADC=90°可知O1(-5,2
),O2(4,
).设图象经过点O1、O2的一次函数解析式为y=kx+b,利用待定系数法可解得直线O1、O2的解析式y=-
x+
.
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
3
| ||
| 2 |
| 27 |
| 4 |
3
| ||
| 2 |
(2)由(1)得r1+r2=3
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 9 |
13
| ||
| 9 |
解答: 解:(1)当l∥x轴时,⊙O1、⊙O2的面积之和最小.
解:(1)当l∥x轴时,⊙O1、⊙O2的面积之和最小.
如图,设切点分别为M、N、D、G.
由切线长定理得MN+DG=AB+BC+AC=18.
∵MN=DG,
∴DG=9,
∴DB+CG=3.
连接O1D、O1B,
∴O1D⊥BD,∠DBO1=60°,
∴DB=
r1.
同理CG=
r2.
∴r1+r2=3
.
∵⊙O1、⊙O2的面积之和S=πr12+π(3
-r1)2
=2π[(r1-
)2+
]
∴当r1=r2=
,即l∥x轴时,S最小.
(2)由(1)得r1+r2=3
,
∵r1-r2=
,∠BDH=∠ADC=90°,
∴O1(-5,2
),O2(4,
).
设图象经过点O1、O2的一次函数解析式为y=kx+b,
则
,
解得
∴直线O1、O2的解析式为y=-
x+
.
 解:(1)当l∥x轴时,⊙O1、⊙O2的面积之和最小.
解:(1)当l∥x轴时,⊙O1、⊙O2的面积之和最小. 如图,设切点分别为M、N、D、G.
由切线长定理得MN+DG=AB+BC+AC=18.
∵MN=DG,
∴DG=9,
∴DB+CG=3.
连接O1D、O1B,
∴O1D⊥BD,∠DBO1=60°,
∴DB=
| ||
| 3 |
同理CG=
| ||
| 3 |
∴r1+r2=3
| 3 |
∵⊙O1、⊙O2的面积之和S=πr12+π(3
| 3 |
=2π[(r1-
3
| ||
| 2 |
| 27 |
| 4 |
∴当r1=r2=
3
| ||
| 2 |
(2)由(1)得r1+r2=3
| 3 |
∵r1-r2=
| 3 |
∴O1(-5,2
| 3 |
| 3 |
设图象经过点O1、O2的一次函数解析式为y=kx+b,
则
|
解得
|
∴直线O1、O2的解析式为y=-
| ||
| 9 |
13
| ||
| 9 |
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象上点的意义和圆中的有关性质来表示相应的线段之间的关系,利用切线长和半径的特点找到相等关系利用方程组求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.

练习册系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.