题目内容
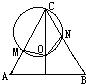 25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.
25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.分析:连接AO,由于正三角形ABC的边长为3,故求得AM=CN=1,由CO是正△ABC的一条对称轴?∠ACO=∠NCO,由圆周角定理知,MO=NO,又由圆内接四边形的外角等于它的内对角知,∠AMO=∠CNO,可由SAS证得,△AMO≌△CNO?∠MAO=∠NCO=30°,即点O是正△ABC两个内角平分线的交点,所以点O是正△ABC的中心.
解答: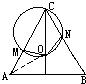 解:如图,连接AO,(1分)
解:如图,连接AO,(1分)
在△AMO和△CNO中,AM=CN=1,
∵CD是正△ABC的一条对称轴,
∴∠ACO=∠NCO.
∴MO=NO.
又∠AMO=∠CNO,
∴△AMO≌△CNO.(5分)
∴∠MAO=∠NCO=30°.
∴O是正△ABC两个内角平分线的交点.
∴点O是正△ABC的中心.(7分)
 解:如图,连接AO,(1分)
解:如图,连接AO,(1分)在△AMO和△CNO中,AM=CN=1,
∵CD是正△ABC的一条对称轴,
∴∠ACO=∠NCO.
∴MO=NO.
又∠AMO=∠CNO,
∴△AMO≌△CNO.(5分)
∴∠MAO=∠NCO=30°.
∴O是正△ABC两个内角平分线的交点.
∴点O是正△ABC的中心.(7分)
点评:本题利用了等边三角形的性质,全等三角形的判定和性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
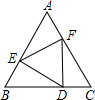 如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
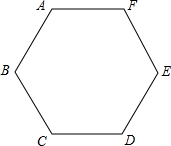 已知:如图,边长为a的正六边形ABCDEF.
已知:如图,边长为a的正六边形ABCDEF.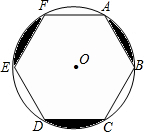 如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为
如图,边长为2的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为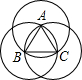 如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为
如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为 如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )
如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )