题目内容
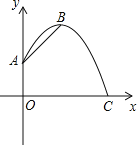
【题目】一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
【答案】(1)2+![]() ;(2)
;(2)![]() 秒 .
秒 .
【解析】试题分析:(1)作BD⊥y轴于点D,由∠DAB=45°,就可以求出AD=BD=2,就可以求出B的坐标,设抛物线的解析式为y=a(x-2)2+3.5,由待定系数法求出其解析式,把y=0时代入解析式求出其解即可;
(2)当y=2时代入(1)的解析式求出x的值,再将x的值代入t=0.8x求出t的值即可.
试题解析:(1)作BD⊥y轴于点D,
∴∠ADB=90°,
∵∠DAB=45°,
∴∠ABD=∠DBA=45°,
∴AD=BD=2,
∴B(2,3.5),
∵OA=1.5,
∴A(0,1.5),
设抛物线的解析式为y=a(x-2)2+3.5,由题意,得
1.5=4a+3.5,
解得:a=-0.5,
∴y=-0.5(x-2)2+3.5,
当y=0时,0=-0.5(x-2)2+3.5,
解得:x1=2+![]() ,x2=2-
,x2=2-![]() (舍去),
(舍去),
∴水流落地点C到O点的距离为(2+![]() )米;
)米;
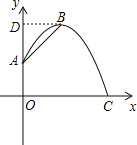
(2)当y=2时,
2=-0.5(x-2)2+3.5.
解得:x1=2+![]() ,x2=2-
,x2=2-![]() ,
,
∴水流位移的距离为:2+![]() -(2-
-(2-![]() )=2
)=2![]() ,
,
∴t=0.8×2![]() =
=![]() 秒
秒
即共有![]() 秒钟,水流高度不低于2米.
秒钟,水流高度不低于2米.

练习册系列答案
相关题目