题目内容
 如图,二次函数
如图,二次函数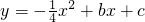 的图象经过点A(4,0),B(-4,-4),且与y轴交于点C.
的图象经过点A(4,0),B(-4,-4),且与y轴交于点C.
(1)试求此二次函数的解析式;
(2)试证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
 解:(1)∵点A(4,0)与B(-4,-4)在二次函数图象上,
解:(1)∵点A(4,0)与B(-4,-4)在二次函数图象上,∴
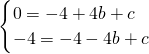
解得
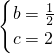
∴二次函数解析式为y=-
 x2+
x2+ x+2.
x+2.(2)过B作BD⊥x轴于点D,由(1)得C(0,2),
则在Rt△AOC中,tan∠CAO=
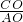 =
=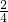 =
= ,
,又在Rt△ABD中,tan∠BAD=
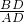 =
=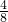 =
= ;
;∵tan∠CAO=tan∠BAD,
∴∠CAO=∠BAO.
(3)由点A(4,0)与B(-4,-4),可得直线AB的解析式为y=
 x-2,
x-2,设P(x,
 x-2),(-4<x<4);
x-2),(-4<x<4);则Q(x,-
 x2+
x2+ x+2),
x+2),∴PH=|
 x-2|=2-
x-2|=2- x,QH=|-
x,QH=|- x2+
x2+ x+2|.
x+2|.∴2-
 x=2|-
x=2|- x2+
x2+ x+2|.
x+2|.当2-
 x=-
x=- x2+x+4,
x2+x+4,解得x1=-1,x2=4(舍去),
∴P(-1,-
 )
)当2-
 x=
x= x2-x-4,
x2-x-4,解得x1=-3,x2=4(舍去),
∴P(-3,-
 ).
).综上所述,存在满足条件的点,它们是P1(-1,-
 )与P2(-3,-
)与P2(-3,- ).
).分析:(1)由于抛物线的解析式中只有两个待定系数,因此只需将A、B两点的坐标代入抛物线中即可求出二次函数的解析式.
(2)本题可先根据抛物线的解析式求出C点的坐标,然后根据这三点的坐标,求出∠CAO和∠BAO的正切值,以此来证明这两角相等.
(3)可先根据直线AB的解析式设出P点的坐标,由于PH⊥x轴,因此P、Q两点的横坐标相等,可根据抛物线的解析式求出Q点的纵坐标,根据PH=2QH,即P的纵坐标的绝对值是Q的纵坐标绝对值的2倍,由此可求出P、Q的横坐标,进而可求出P点的坐标.
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).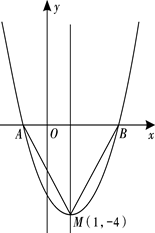
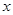 轴的交点A,B的坐标;
轴的交点A,B的坐标; 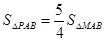 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;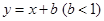 与此图象有两个公共点时,
与此图象有两个公共点时,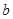 的取值范围.
的取值范围.