题目内容
把两个大小不同的等腰直角三角形三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
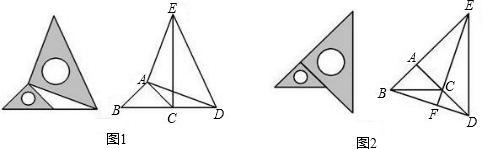
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
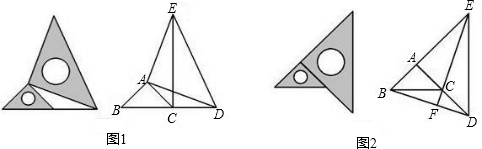
(1)图1是一种放置位置及由它抽象出的几何图形,B、C、D在同一条直线上,连接EC.请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
(2)图2也是一种放置位置及由它抽象出的几何图形,A、C、D在同一条直线上,连接BD、连接EC并延长与BD交于点F.请找出线段BD和EC的位置关系,并说明理由;
(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段BD和EC的位置和数量关系;
③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?

(1)△ABD≌△ACE.(1分)
∵△ABC是直角三角形,
∴AB=AC,∠BAC=90°.(1分)
同理 AD=AE,∠EAD=90°.(1分)
∴∠BAC=∠EAD.
∴∠BAC+∠CAD=∠EAD+∠CAD.
即∠BAD=∠CAE.(1分)
在△ABD和△ACE中,
∴△ABD≌△ACE.
(2)在△ABD和△ACE中,
∴△ABD≌△ACE.
∴∠ADB=∠AEC.(全等三角形对应角相等)(1分)
∵∠ACE=∠DCF,(对顶角相等)
∠ADB+∠DCF+∠EFD=180°,(三角形内角和180°)
∠AEC+∠ACE+∠EAC=180°,(三角形内角和180°)(1分)
∴∠EAC=∠EFD.(1分)
∵∠BAC=90°,

∴∠EAC=90°.
即∠EFD=90°.
∴BD⊥EC.(垂直定义)(1分)
(3)①如图:(1分)
②BD=EC,BD⊥EC.(2分)
③存在.(1分)
∵△ABC是直角三角形,
∴AB=AC,∠BAC=90°.(1分)
同理 AD=AE,∠EAD=90°.(1分)
∴∠BAC=∠EAD.
∴∠BAC+∠CAD=∠EAD+∠CAD.
即∠BAD=∠CAE.(1分)
在△ABD和△ACE中,
|
∴△ABD≌△ACE.
(2)在△ABD和△ACE中,
|
∴△ABD≌△ACE.
∴∠ADB=∠AEC.(全等三角形对应角相等)(1分)
∵∠ACE=∠DCF,(对顶角相等)
∠ADB+∠DCF+∠EFD=180°,(三角形内角和180°)
∠AEC+∠ACE+∠EAC=180°,(三角形内角和180°)(1分)
∴∠EAC=∠EFD.(1分)
∵∠BAC=90°,

∴∠EAC=90°.
即∠EFD=90°.
∴BD⊥EC.(垂直定义)(1分)
(3)①如图:(1分)
②BD=EC,BD⊥EC.(2分)
③存在.(1分)

练习册系列答案
相关题目