题目内容
 将
将 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是
沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是
- A.3

- B.8
- C.
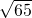
- D.2
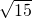
A
分析:若连接CD、AC,则根据同圆或等圆中,相等的圆周角所对的弦相等,求得AC=AD;过C作AB的垂线,设垂足为E,则DE= AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
解答: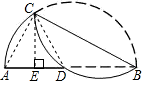 解:连接CA、CD;
解:连接CA、CD;
根据折叠的性质,知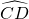 所对的圆周角等于∠CBD,
所对的圆周角等于∠CBD,
又∵ 所对的圆周角是∠CBA,
所对的圆周角是∠CBA,
∵∠CBD=∠CBA,
∴AC=CD(相等的圆周角所对的弦相等);
∴△CAD是等腰三角形;
过C作CE⊥AB于E.
∵AD=4,则AE=DE=2;
∴BE=BD+DE=7;
在Rt△ACB中,CE⊥AB,根据射影定理,得:
BC2=BE•AB=7×9=63;
故BC=3 .
.
故选A.
点评:此题考查的是折叠的性质、圆周角定理、以及射影定理;能够根据圆周角定理来判断出△ACD是等腰三角形,是解答此题的关键.
分析:若连接CD、AC,则根据同圆或等圆中,相等的圆周角所对的弦相等,求得AC=AD;过C作AB的垂线,设垂足为E,则DE=
 AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.解答:
 解:连接CA、CD;
解:连接CA、CD;根据折叠的性质,知
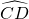 所对的圆周角等于∠CBD,
所对的圆周角等于∠CBD,又∵
 所对的圆周角是∠CBA,
所对的圆周角是∠CBA,∵∠CBD=∠CBA,
∴AC=CD(相等的圆周角所对的弦相等);
∴△CAD是等腰三角形;
过C作CE⊥AB于E.
∵AD=4,则AE=DE=2;
∴BE=BD+DE=7;
在Rt△ACB中,CE⊥AB,根据射影定理,得:
BC2=BE•AB=7×9=63;
故BC=3
 .
.故选A.
点评:此题考查的是折叠的性质、圆周角定理、以及射影定理;能够根据圆周角定理来判断出△ACD是等腰三角形,是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 将
将 |
| BC |
A、3
| ||
| B、8 | ||
C、
| ||
D、2
|
 将弧BC沿弦BC折叠交直径AB于点D,若AD=4,DB=5,则BC的长是
将弧BC沿弦BC折叠交直径AB于点D,若AD=4,DB=5,则BC的长是 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )



 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )


