题目内容
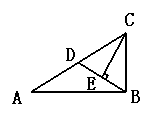
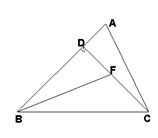
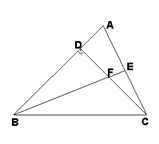
如图,已知在等腰直角三角形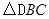 中,
中,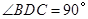 ,
, 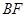 平分
平分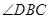 ,与
,与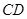 相交于点
相交于点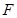 ,延长
,延长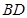 到
到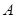 ,使
,使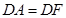 ,
,
(1)求证: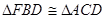 ;
;
(2)延长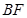 交
交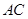 于
于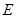 ,且
,且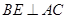 ,求证:
,求证: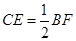 ;
;
(3)在⑵的条件下,若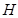 是
是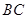 边的中点,连结
边的中点,连结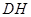 与
与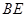 相交于点
相交于点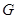 .
.
试探索 ,
,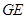 ,
,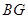 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.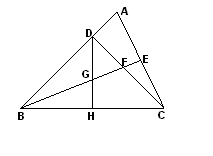
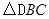 中,
中,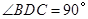 ,
, 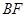 平分
平分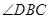 ,与
,与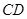 相交于点
相交于点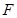 ,延长
,延长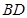 到
到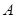 ,使
,使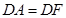 ,
,(1)求证:
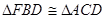 ;
;
(2)延长
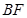 交
交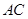 于
于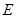 ,且
,且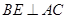 ,求证:
,求证: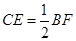 ;
;
(3)在⑵的条件下,若
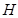 是
是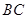 边的中点,连结
边的中点,连结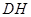 与
与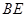 相交于点
相交于点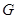 .
.试探索
 ,
,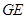 ,
,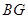 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(1)∵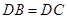 ,
,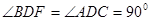
又∵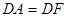 ;
;
∴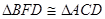 ,--------------------------3分
,--------------------------3分
(2)∴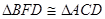 ,∴
,∴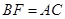
又∵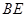 平分
平分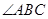 ,∴
,∴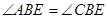
又∵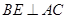 ,∴
,∴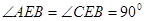 ,
,
又∵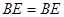
∴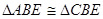 ,∴
,∴
∴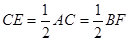 ----------------------------- 7分
----------------------------- 7分
(3) ,
,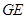 ,
,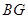 之间的数量关系为:
之间的数量关系为: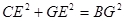
连结CG,∵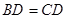 ,H是
,H是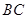 边的中点,
边的中点,
∴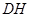 是
是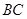 的中垂线,
的中垂线,
∴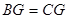 在
在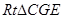 中有:
中有: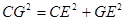
∴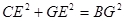 -------------------------------------------------10分
-------------------------------------------------10分
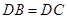 ,
,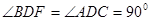
又∵
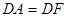 ;
;∴
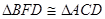 ,--------------------------3分
,--------------------------3分(2)∴
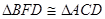 ,∴
,∴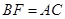
又∵
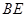 平分
平分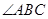 ,∴
,∴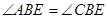
又∵
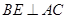 ,∴
,∴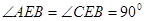 ,
,又∵
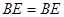
∴
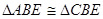 ,∴
,∴
∴
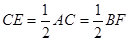 ----------------------------- 7分
----------------------------- 7分(3)
 ,
,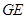 ,
,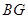 之间的数量关系为:
之间的数量关系为: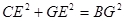
连结CG,∵
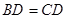 ,H是
,H是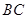 边的中点,
边的中点,∴
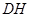 是
是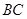 的中垂线,
的中垂线,∴
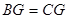 在
在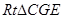 中有:
中有: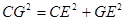
∴
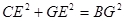 -------------------------------------------------10分
-------------------------------------------------10分(1)由已知等腰直角三角形△DBC可推出DB=DC,且∠BDF=∠ADC=90°,与已知DA=DF通过SAS证得△FBD≌△ACD;
(2)先由(1)△FBD≌△ACD得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=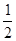 AC,从而得出结论;
AC,从而得出结论;
(3)连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角三角形CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
(2)先由(1)△FBD≌△ACD得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=
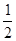 AC,从而得出结论;
AC,从而得出结论;(3)连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角三角形CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.

练习册系列答案
相关题目