题目内容
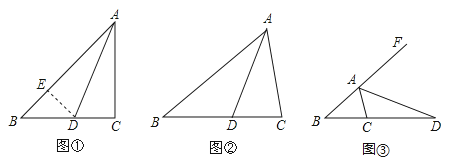
【题目】在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;
(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;
②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.
【答案】(1)证明见解析;(2)①AB=AC+CD;②AC+AB=CD,证明见解析.
【解析】
(1)首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE=45°,求出BE=DE=CD,进而得出答案;
(2)①首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE,求出BE=DE=CD,进而得出答案;
②首先得出△AED≌△ACD(SAS),即可得出∠B=∠EDC,求出BE=DE=CD,进而得出答案.
解:(1)∵AD为∠ABC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠C=∠AED=90°,
∵∠ACB=2∠B,∠C=90°,
∴∠B=45°,∴∠BDE=45°,
∴BE=ED=CD,
∴AB=AE+BE=AC+CD;
(2)①AB=AC+CD.
理由:在AB上截取AE=AC,连接DE,
∵AD为∠ABC的角平分线,∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠C=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠B+∠BDE=∠AED,
∴∠B=∠BDE,∴BE=ED=CD,
∴AB=AE+BE=AC+CD;
②AC+AB=CD.
理由:在射线BA上截取AE=AC,连接DE,
∵AD为∠EAC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠ACD=∠AED,
∵∠ACB=2∠B,
∴设∠B=x,则∠ACB=2x,∴∠EAC=3x,∴∠EAD=∠CAD=1.5x,
∵∠ADC+∠CAD=∠ACB=2x,∴∠ADC=0.5x,∴∠EDC=x,
∴∠B=∠EDC,∴BE=ED=CD,
∴AB+AE=BE=AC+AB=CD.

【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误



