Question

19、某中学为了让学生了解环保知识，增强环保意识，特地举行了一次“健康饮水，保护水源”的环保知识竞赛，共有900名学生参加这次竞赛．为了解本次竞赛的情况，从中抽取了部分学生的成绩（得分均为正整数，满分为100分）进行统计．

分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5	8	0.16
70.5～80.5	10	0.20
80.5～90.5	16	0.32
90.5～100	12	0.24
合计	50	1

     频率分布表
请根据上述内容，解答下列问题：
（1）填充频率分布表中的空格并补全频率分布直方图；
（2）全体参赛学生中，竞赛成绩的中位数落在哪个组内？
（3）若成绩在80分以上（不含80分）可以获奖，在全校学生的试卷中任抽取一张，获奖的概率是多大？

Answer 1

分析：（1）先求出抽取学生的人数和90.5～100的频率，再根据频率公式求出90.5～100的频数，补全频率分布直方图；
（2）根据中位数的求法：给定n个数据，按从小到大排序，如果n为奇数，位于中间的那个数就是中位数；如果n为偶数，位于中间两个数的平均数就是中位数．知中位数落在80.5～90.5；
（3）成绩在80分以上（不含80分）的应是后2组，由随机事件A的概率P（A）=$frac{事件A可能出现的结果数}{所有可能出现的结果数}$求解即可．

解答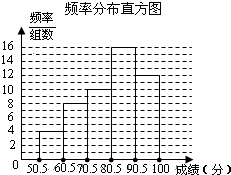：解：（1）

分组	频数	频率
50.5～60.5
60.5～70.5
70.5～80.5
80.5～90.5
90.5～100	12	0.24
合计	50	1

（4分）（正确填表（2分），正确补全直方图2分）
（2）50个数据，按次序排列后，中位数应是第25个和第26个数据的平均数，第25个和第26个数据都在80.5～90.5内，故全体参赛学生中，竞赛成绩的中位数落在80.5～90.5内；（6分）
（3）（16+12）÷50×100%=56%．
故获奖的概率是56%．（9分）

点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力，同时考查中位数、概率的求法：给定n个数据，按从小到大排序，如果n为奇数，位于中间的那个数就是中位数；如果n为偶数，位于中间两个数的平均数就是中位数．任何一组数据，都一定存在中位数的，但中位数不一定是这组数据量的数．