Question

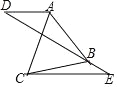
【题目】如图，直线DE过等边△ABC的顶点B，连接AD、CE，AD∥CE，∠E=30°，若BE：AD=1：，CE=时，则BC= ．

Answer 1

【答案】．

【解析】

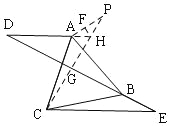
试题分析：将△CBE绕C逆时针旋转60°到△CAP，BC与AC重合，延长DA交PC于H，过H作HF⊥AP于F，CP交DE于G，

∴∠PCE=60°，

∵∠E=30°，

∴∠CGE=90°，

由旋转得：CE=CP，

Rt△CGE中，CE=CP=，

∴CG=CE=，

∴GP=PC﹣CG=，

∵AD：BE=：1，

设AD=x，BE=x，则AP=BE=x，

∵AD∥BE，

∴∠ADE=∠E=30°，

Rt△DGH中，∠DHG=60°，

由旋转得：∠APC=∠E=30°，

∴∠HAP=60°﹣30°=30°，

∴∠HAP=∠APC=30°，

∴AH=PH，AF=PF=x，

cos30°=，

∴PH==x，

∴DH=AD+AH=x+x=x，

∴GH=DH=x，

∵PG==GH+PH，

∴2=x+x，

x=2，

∴BE=x=2，

由勾股定理得：EG===6，

∴BG=6﹣2=4，

在Rt△BGC中，BC===；