Question

【题目】（1）若正整数、，满足，求、的值；

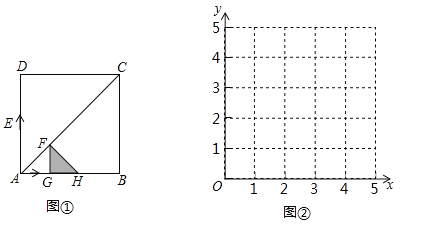
（2）已知如图，在中，，，点在边上移动（不与点，点重合），将沿着直线翻折，点落在射线上点处，当为一个含内角的直角三角形时，试求的长度．

Answer 1

【答案】（1）或；（2）或．

【解析】

（1）根据平方差公式因式分解，根据题意可得或；

（2）根据翻折性质可证∠AEF=180°∠BEF =90°，分两种情况：①如图a，当∠EAF=30°时，设BD=x，根据勾股定理，即；②如图b，当∠AFE=30°时，设BD=x，根据勾股定理，，；

（1）解：∵>0，且x，y均为正整数，

∴与均为正整数，且>，与奇偶性相同．

又∵

∴或

解得：或．

（2）解：∵∠ACB=90°，AC=BC∴∠B=∠BAC=45°

又∵将△BDE沿着直线DE翻折，点B落在射线BC上点F处

∴∠BDE=∠EDF=90°，且△BDE≌△FDE

∴∠BED=∠DEF=45°，∠BEF=90°，BE=EF

∴∠AEF=180°∠BEF =90°

①如图a，当∠EAF=30°时，设BD=x，则：

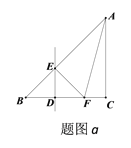
BD=DF=DE=x，，，

∵∠EAF=30°，∴AF=，

在Rt△AEF中，，

∴，解得．

∴．

②如图b，当∠AFE=30°时，设BD=x，则：

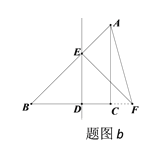
同理①可得：，

∵∠AFE =30°，∴AF=

在Rt△AEF中，，

∴，解得．

∴．

综上所述，或．