题目内容
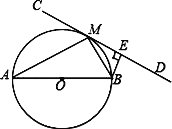
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.
【答案】(1)证明见解析;(2)证明见解析;(3)8.
【解析】试题分析:(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,
(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
试题解析:(1)如图,连接OM,
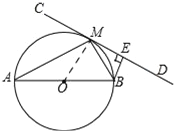
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB;
(2)由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴![]()
∴BM2=BEAB;
(3)由(1)有,∠BME=∠MAB,
∵sin∠BAM=![]() ,
,
∴sin∠BME=![]() ,
,
在Rt△BEM中,BE=![]() ,
,
∴sin∠BME=![]() =
=![]() ,
,
∴BM=6,
在Rt△ABM中,sin∠BAM=![]() ,
,
∴sin∠BAM=![]() =
=![]() ,
,
∴AB=![]() BM=10,据勾股定理得,AM=8.
BM=10,据勾股定理得,AM=8.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目