题目内容
●观察计算当a=5，b=3时，
| a+b |
| 2 |
| ab |
当a=4，b=4时，
| a+b |
| 2 |
| ab |
●探究证明
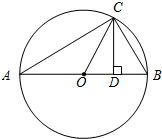
如图所示，△ABC为圆O的内接三角形，AB为直径，过C作CD⊥AB于D，设AD=a，BD=b．
（1）分别用a，b表示线段OC，CD；
（2）探求OC与CD表达式之间存在的关系（用含a，b的式子表示）．
●归纳结论
根据上面的观察计算、探究证明，你能得出
| a+b |
| 2 |
| ab |
●实践应用
要制作面积为1平方米的长方形镜框，直接利用探究得出的结论，求出镜框周长的最小值．
分析：●观察计算：分别代入计算即可得出
与
的大小关系；
●探究证明：
（1）由于OC是直径AB的一半，则OC易得．通过证明△ACD∽△CBD，可求CD；
（2）分a=b，a≠b讨论可得出
与
的大小关系；
●实践应用：通过前面的结论长方形为正方形时，周长最小．
| a+b |
| 2 |
| ab |
●探究证明：
（1）由于OC是直径AB的一半，则OC易得．通过证明△ACD∽△CBD，可求CD；
（2）分a=b，a≠b讨论可得出
| a+b |
| 2 |
| ab |
●实践应用：通过前面的结论长方形为正方形时，周长最小．
解答：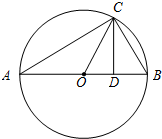
解：●观察计算：
＞
，
=
．
●探究证明：
（1）∵AB=AD+BD=2OC，
∴OC=
∵AB为⊙O直径，
∴∠ACB=90°．
∵∠A+∠ACD=90°，∠ACD+∠BCD=90°，
∴∠A=∠BCD．
∴△ACD∽△CBD．
∴
=
．
即CD2=AD•BD=ab，
∴CD=
．
（2）当a=b时，OC=CD，
=
；
a≠b时，OC＞CD，
＞
．
●结论归纳：
≥
．
●实践应用
设长方形一边长为x米，则另一边长为
米，设镜框周长为l米，则l=2(x+
)≥4
=4．
当x=
，即x=1（米）时，镜框周长最小．
此时四边形为正方形时，周长最小为4米．
解：●观察计算：| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
●探究证明：
（1）∵AB=AD+BD=2OC，
∴OC=
| a+b |
| 2 |
∵AB为⊙O直径，
∴∠ACB=90°．
∵∠A+∠ACD=90°，∠ACD+∠BCD=90°，
∴∠A=∠BCD．
∴△ACD∽△CBD．
∴
| AD |
| CD |
| CD |
| BD |
即CD2=AD•BD=ab，
∴CD=
| ab |
（2）当a=b时，OC=CD，
| a+b |
| 2 |
| ab |
a≠b时，OC＞CD，
| a+b |
| 2 |
| ab |
●结论归纳：
| a+b |
| 2 |
| ab |
●实践应用
设长方形一边长为x米，则另一边长为
| 1 |
| x |
| 1 |
| x |
x•
|
当x=
| 1 |
| x |
此时四边形为正方形时，周长最小为4米．
点评：本题综合考查了几何不等式，相似三角形的判定与性质，通过计算和证明得出结论：
≥
是解题的关键．
| a+b |
| 2 |
| ab |
练习册系列答案
名校课堂系列答案
相关题目
附加题．观察计算
与
的大小关系是
●探究证明
．
与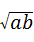
的大小关系是
●探究证明
．
与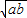
的大小关系是______