题目内容
【题目】如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.
(1)∠DCA与∠EAB相等吗?说明理由;
(2)△ADC与△BEA全等吗?说明理由.
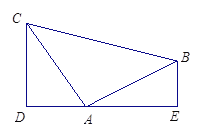
【答案】(1)理由见解析;(2)理由见解析.
【解析】分析:
(1)根据AB⊥AC和CD⊥DE可以求得∠DCA=∠EAB;
(2)根据(1)中的∠DCA=∠EAB和AB=AC可以求证△ADC≌△BEA.
本题解析:
证明:(1)相等.因为AB⊥AC,CD⊥DE,BE⊥DE,
所以∠BAC=∠D=∠E=90°,
所以∠CAD+∠BAE=90°,∠DCA+∠CAD=90°,
所以∠DCA=∠EAB;
(2)全等.在△ADC和△BEA中,
因为∠D=∠E,∠DCA=∠EAB,AC=BA
所以△ADC≌△BEA (AAS).

练习册系列答案
相关题目