题目内容
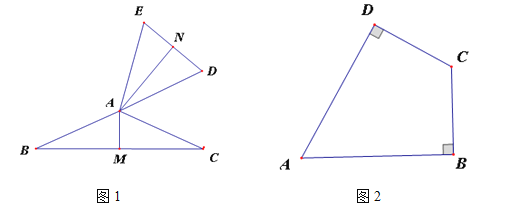
【题目】已知：如图，点C在线段AB上，点M、N分别是AC、BC的中点．
（1）若AC = 8，CB = 6，求线段MN的长；
（2）若AC = a，MN = b，求线段BC的长用含
，
的代数式可以表示．
【答案】（1）MN=7；（2）
．
【解析】
(1)根据“点M、N分别是AC、BC的中点”，先求出MC、CN的长度，再利用MN=CM+CN即可求出MN的长度即可；
(2)由AC=a，得到MC=
，由MN=b，得到CN=b-
，从而求出BC的长.
解：(1)∵AC=8，CB = 6，
∴AB= AC + CB =14．
∵点M、N分别是AC、BC的中点，
∴MC=
AC，NC=BC (线段中点的定义) ，
∴MN=(AC+BC)=7.
(2)线段BC的长用含
，
的代数式可以表示为
．
∵AC=a，M是AC的中点，
∴MC=AC=，
∵MN=b，
∴CN=b-，
∵N是BC的中点，
∴BC=2CN=2(b-)=2b-a.
故答案为：(1)7；(2)2b-a.
练习册系列答案
相关题目
【题目】某中学八年级
班数学课外兴趣小组在探究：“
边形共有多少条对角线”这一问题时，设计了如下表格：
多边形的边数 |
|
|
|
|
| … |
从多边形一个顶点出发可引起的对角线条数 | … | |||||
多边形对角线的总条数 | … |
探究：假若你是该小组的成员，请把你研究的结果填入上表；
猜想：随着边数的增加，多边形对角线的条数会越来越多，从边形的一个顶点出发可引的对角线条数为多少，边形对角线的总条数为多少．
应用：
个人聚会，每不相邻的人都握一次手，共握多少次手？
