题目内容
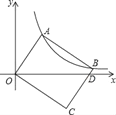
【题目】如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,则AB的长是( )

A. ![]() B. 3 C. 4 D. 5
B. 3 C. 4 D. 5
【答案】A
【解析】
根据平行四边形的性质及平行线的性质可得AB=CD,AD=BC,∠AEB=∠CBE,∠DEC=∠BCE,∠ABC+∠DCB=180°,再由角平分线的定义可得∠ABE=∠CBE=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠DCB,由此即可得∠ABE=∠AEB,∠DCE=∠DEC,∠EBC+∠ECB=90°;根据等腰三角形的判定可得AB=AE,CD=DE,由勾股定理求得BC=5,由此即可求得AB的长.
∠DCB,由此即可得∠ABE=∠AEB,∠DCE=∠DEC,∠EBC+∠ECB=90°;根据等腰三角形的判定可得AB=AE,CD=DE,由勾股定理求得BC=5,由此即可求得AB的长.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠AEB=∠CBE,∠DEC=∠BCE,∠ABC+∠DCB=180°,
∵BE,CE分别是∠ABC和∠BCD的平分线,
∴∠ABE=∠CBE=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠DCB,
∠DCB,
∴∠ABE=∠AEB,∠DCE=∠DEC,∠EBC+∠ECB=90°,
∴AB=AE,CD=DE,
∴AD=BC=2AB,
∵BE=4,CE=3,
∴BC=![]() =5,
=5,
∴AB=![]() BC=
BC=![]() .
.
故选A.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目